线速度与角速度之间的关系

高中物理知识：线速度与角速度之间的关系

1.线速度

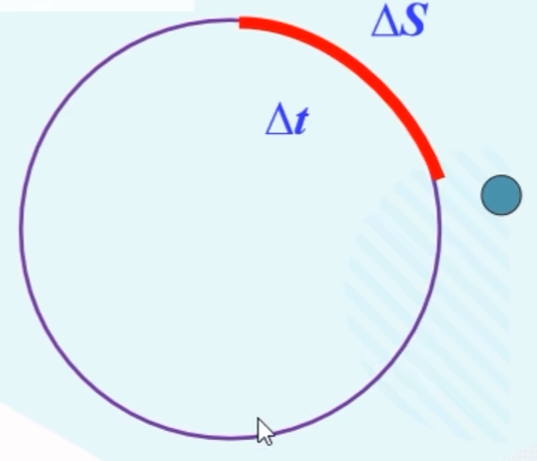
物理意义：描述质点圆周运动快慢的物理量。
定义：质点做圆周运动通过的弧长$\Delta S$和所用时间$\Delta t$的比值叫做线速度的大小。
公式：$v=\frac{\Delta S}{\Delta t}$
单位：$m/s$
方向：质点在圆周某点的线速度方向沿圆周上该点的切线方向。

2.角速度

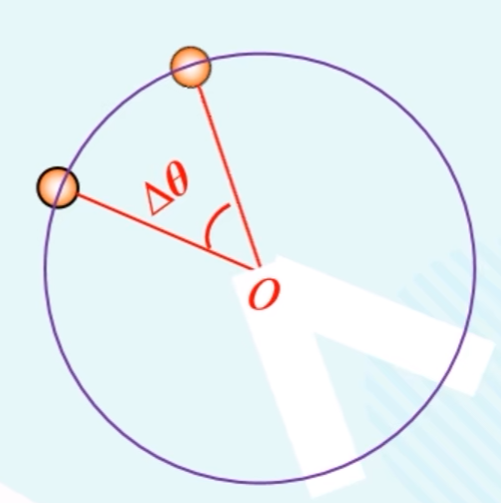
物理意义：描述质点绕圆心转动快慢的物理量。
定义：质点所在半径转过的角度$\Delta \theta$和所用时间$\Delta t$的比值叫做角速度。
公式：$\omega = \frac{\Delta \theta}{\Delta t}$
单位：弧度/秒 $rad/s$

3.关系证明

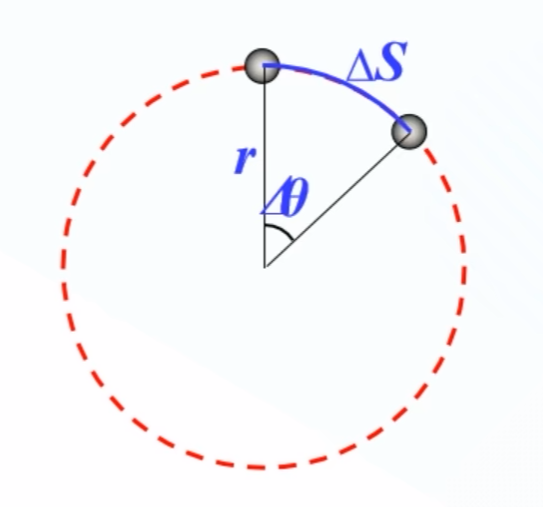
在$\Delta t$内通过的弧长为$\Delta S$，半径转过的角度为$\Delta \theta$
由$\Delta S=r\Delta \theta$
得到$v=\frac{\Delta S}{\Delta t}=\frac{r\Delta \theta}{\Delta t}=\omega r$
写成微分形式$\frac{d\theta}{dt}=\frac{v}{r}$