差速底盘机器人运动分析

1.差速驱动是许多移动轮式机器人的运动控制方式
2.差速驱动机器人通常有两个动力轮，机器人每侧各一个，有时还有其他从动轮以防止机器人倾翻。
3.当两个轮子以相同的速度向相同的方向转动时，机器人沿直线运动。
4.当一个轮子转得比另一个轮子快时，机器人沿弧线运动。
5.当轮子朝以相同大小的速度向相反的方向转动时，机器人就原地转动。
6.我们可以正式描述机器人的行为如下：
 (a) 当机器人沿曲线运动时，存在一个瞬时曲率中心（ICC）。
 (b) 如果$r$表示曲线的半径（ICC到机器人中心的距离），$l$表示机器人的轮距，那么角速度和ICC的关系可以按如下方式推导：

$$\omega(r+\frac{l}{2})=v_r$$ $$\omega(r-\frac{l}{2})=v_l$$

为什么？因为角速度的定义为线速度除以曲线半径：

$$\frac{d\theta}{dt}=\frac{V}{r}$$

上式比较直观的物理的意义是：轮子离中心越远需要移动得越快才能获得与另一个轮子相同的角速度。
通过上式我们得到：

$$v_r=\omega(r+\frac{l}{2})\\=\omega r+\omega \frac{l}{2}$$ $$v_l=\omega(r-\frac{l}{2})\\=\omega r-\frac{l}{2}$$

以上两式相减得到：

$$v_r-v_l=\frac{2\omega l}{2}$$ $$\omega = \frac{v_r-v_l}{l}$$

相加得到：

$$2\omega r=v_r+v_l$$ $$r=\frac{l(v_r+v_l)}{2(v_r-v_l)}$$

综上所述，我们发现：
i.角速度是车轮速度在它们分开的距离内的差异。
ii.如果$v_r=v_l$，那么$\omega$为0，机器人沿直线行走。
iii.如果$v_r=-v_l$，那么$r$为0，机器人原地旋转。

机器人位姿

假设机器人在运行时的位置为x,y ，并且朝向某一角度$\theta$，$\theta$是机器人坐标系$x$轴与世界坐标系$x$轴的夹角。定义$\theta=0$时机器人$x$轴与世界坐标系$x$轴一致。当机器人移动时，机器人的局部坐标系也一同移动，另$x,y,\theta$为机器人的位姿(pose)。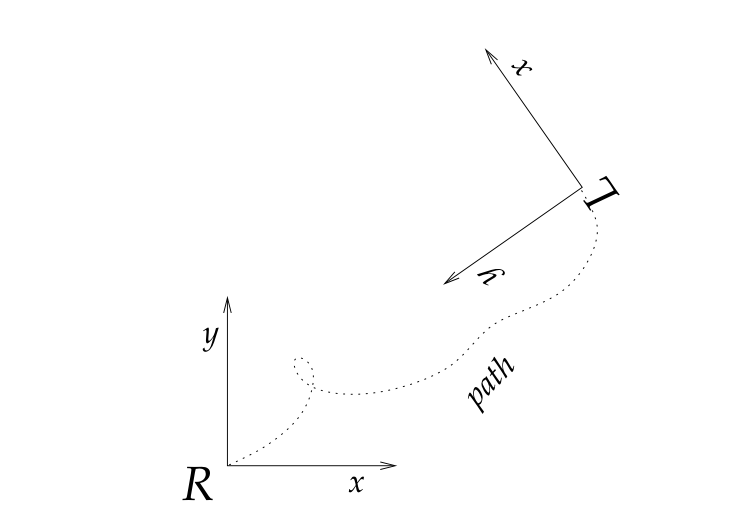

机器人坐标系

前向运动学

给定一个初始位姿，机器人以角速度$\omega$在$\delta t$时间内运动，确定机器人的新位姿。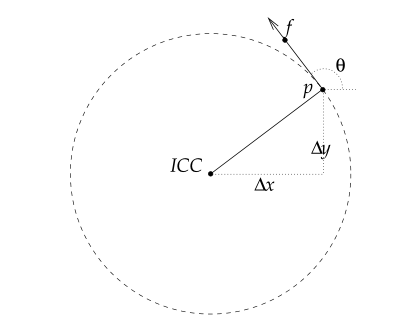

确定机器人新位姿

(a) 首先，注意所有变量都是时间的函数：$x(t)，y(t)，\omega(t)，V(t)，\theta(t)$。
(b) 然后，我们来计算ICC位于何处，得到$r$

未完待续。。。