刚体位姿

引言

 刚体在三维笛卡尔空间的运动包括平移和旋转，平移用三个笛卡尔坐标，旋转用三个角坐标，因此，刚体运动需要六个坐标。机器人运动学研究的就是在空间中不断地去控制机器人的位置和方向，为了确定机器人的位置和方向，需要建立一个固定的参考坐标系，称为固定坐标系或世界坐标系。另外，在移动的机器人上需建立一个移动坐标系或局部坐标系来描述机器人的位姿。
 按照参考坐标系来看，刚体的位置和方向有六个独立的参数，如下图所示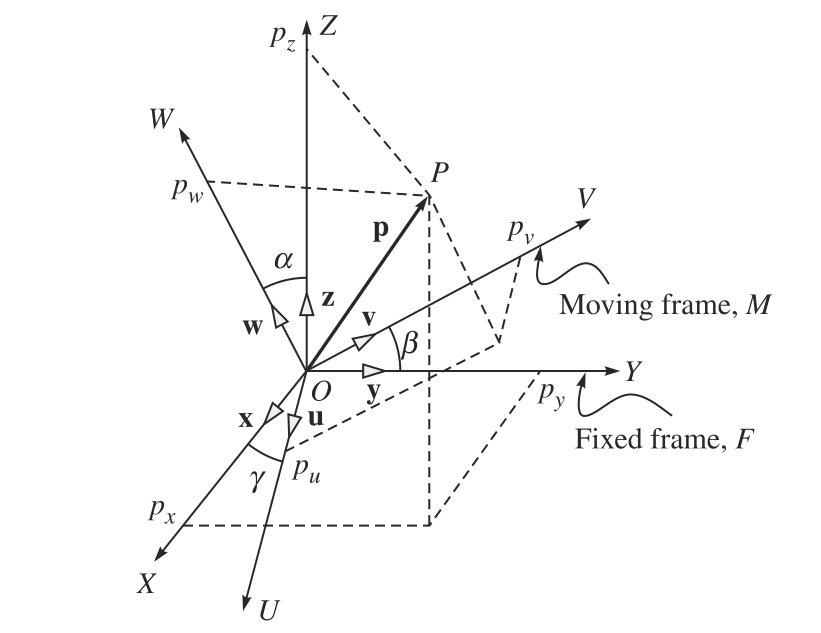

定义$X-Y-Z$坐标系为固定坐标系，机器人在运动过程中建立的运动坐标系为$U-V-W$，很明显，如果确定了运动坐标系相对于固定坐标系的位姿，那么刚体的位姿也就知道了。刚体位姿可以通过刚体上任意一点的位姿来确定，例如原点$O$或刚体上任一点$P$。

位置描述

 运动中的刚体上任何一点$P$相对于固定坐标系的位置可以用一个三维笛卡尔向量P，如上图所示，定义点$P$在固定坐标系$F$中的坐标或向量P在固定坐标系$F$的分量为$p_x,p_y,p_z$为

$$\left[ \mathbf{P}\right]_F=\left[ \begin{matrix} p_x\\ p_y \\ p_z \end{matrix} \right] \tag{1}$$

这里的下表$F$表示向量P参考的固定坐标系。
 下表$x,y,z$分别表示向量P沿固定坐标系$X,Y,Z$三个方向的分量。
 向量P可以表达为：

$$\mathbf{P}=p_x\mathbf{x}+p_y\mathbf{y}+p_z\mathbf{z} \tag{2}$$

这里$\mathbf{x},\mathbf{y},\mathbf{z}$分别表示沿固定坐标系$F$的$X,Y,Z$方向的单位向量，如上图所示。在固定坐标系$F$下分别写为：

$$\left[ \mathbf{x} \right]_F\equiv\left[ \begin{matrix}1\\0\\0\end{matrix}\right], \left[ \mathbf{y} \right]_F\equiv\left[ \begin{matrix}0\\1\\0\end{matrix}\right], and \left[ \mathbf{z} \right]_F\equiv\left[ \begin{matrix}0\\0\\1\end{matrix}\right]\tag{3}$$

注意：如果向量P参考的固定坐标系是不同于坐标系$F$的，那么，向量P的分量将会不同于参考固定坐标系$F$的分量，尽管向量P没变，因此，无论参考坐标系如何改变，向量P是不会变的，这就是所谓的坐标无关的表达方式，也可以说是与参考系是独立的。

方向描述

 根据参考坐标系，刚体的方向可以有不同的描述方式，例如：
1.Direction cosine representation
2.Fixed-axes rotations
3.Euler-angles representation
4.Single- and double-axes rotations
5.Euler parameters, and others
注意：每种描述方式都有其局限，下面具体介绍

1.Direction Cosine Representation

 为了描述刚体的方向或旋转，考虑相对于固定坐标系$F$运动的移动坐标系$M$，如图1所示。另$\mathbf{u}、\mathbf{v}、\mathbf{w}$分别表示沿运动坐标系$M$方向$U、V、W$的单位向量，由于每个单位向量$\mathbf{u}、\mathbf{v}、\mathbf{w}$表示点在坐标系$M$下距原点单位距离处的位置，因此，可以用它们各自沿固定坐标系$X、Y、Z$方向的分量来表达：

$$\mathbf{u}=u_x\mathbf{x}+u_y\mathbf{y}+u_z\mathbf{z}\tag{4}$$ $$\mathbf{v}=v_x\mathbf{x}+v_y\mathbf{y}+v_z\mathbf{z}\tag{5}$$ $$\mathbf{w}=w_x\mathbf{x}+w_y\mathbf{y}+w_z\mathbf{z}\tag{6}$$

这里$u_x、u_y、u_z$分别表示单位向量$\mathbf{u}$沿$X、Y、Z$方向的分量，相似的，$v_x、v_y、v_z$和$w_x、w_y、w_z$分别表示单位向量$\mathbf{v}$和$\mathbf{w}$的分量。现在，如图1所示刚体上的一点$P$在运动坐标系下的表达为：

$$\mathbf{P}=p_u\mathbf{u}+p_v\mathbf{v}+p_w\mathbf{w}\tag{7}$$

这里$p_u,p_v,p_w$分别是向量P沿运动坐标系$M$的坐标轴$U、V、W$的分量，把公式（4）-（6）带入公式（7）得到：

$$\mathbf{P}=(p_uu_x+p_vv_x+p_ww_x)\mathbf{x}+(p_uu_y+p_vv_y+p_ww_y)\mathbf{y}+(p_uu_z+p_vv_z+p_ww_z)\mathbf{z}\tag{8}$$

对比公式（7）和（8）得到：

$$p_x = p_uu_x+p_vv_x+p_ww_x\tag{9}$$ $$p_y = p_uu_y+p_vv_y+p_ww_y\tag{10}$$ $$p_z = p_uu_z+p_vv_z+p_ww_z\tag{11}$$

写成矩阵形式：

$$\left[ \mathbf{p}\right]_F=\mathbf{Q}\left[ \mathbf{p}\right]_M\tag{12}$$

这里$\left[ \mathbf{p}\right]_F$和$\left[ \mathbf{p}\right]_M$分别表示三维向量P在坐标系$F$和$M$的分量，$\mathbf{Q}$是一个$3\times3$的旋转矩阵表示向量P从坐标系$M$到坐标系$F$的转换。它们的具体形式为：

$$\left[ \mathbf{p} \right]_F\equiv\left[ \begin{matrix}p_x\\p_y\\p_z\end{matrix}\right], \left[ \mathbf{p} \right]_M\equiv\left[ \begin{matrix}p_u\\p_v\\p_w\end{matrix}\right], and \left[ \mathbf{Q} \right]\equiv\left[ \begin{matrix}u_x&v_x& w_x\\u_y&v_y& w_y\\u_z&v_z& w_z\end{matrix}\right]=\left[ \begin{matrix}\mathbf{u}^T\mathbf{x}&\mathbf{v}^T\mathbf{x}& \mathbf{w}^T\mathbf{x}\\\mathbf{u}^T\mathbf{y}&\mathbf{v}^T\mathbf{y}& \mathbf{w}^T\mathbf{y}\\\mathbf{u}^T\mathbf{z}&\mathbf{v}^T\mathbf{z}& \mathbf{w}^T\mathbf{z}\end{matrix}\right]\tag{13}$$

注意矩阵$\mathbf{Q}$的每一列都是正交的，它们是单位向量$\mathbf{u},\mathbf{v},\mathbf{w}$在坐标系$F$下的分量，而且必须满足如下的六个正交条件：

$$\mathbf{u}^T\mathbf{u}=\mathbf{v}^T\mathbf{v}=\mathbf{w}^T\mathbf{w}=1,and\mathbf{u}^T\mathbf{v}(\equiv\mathbf{v}^T\mathbf{u})=\mathbf{u}^T\mathbf{w}(\equiv\mathbf{w}^T\mathbf{u})=\mathbf{v}^T\mathbf{w}(\equiv\mathbf{w}^T\mathbf{v})=0\tag{14}$$

并且，对于正交向量$\mathbf{u},\mathbf{v},\mathbf{w}$满足如下关系：

$$\mathbf{u}\times\mathbf{v}=\mathbf{w},\mathbf{v}\times\mathbf{w}=\mathbf{u},and \mathbf{w}\times\mathbf{u}=\mathbf{v}\tag{15}$$

因此，$3\times3$的旋转矩阵$\mathbf{Q}$，给出了运动坐标系$M$相对于固定坐标系$F$的方位，就是所谓的正交矩阵。它有如下特性：

$$\mathbf{Q}^T\mathbf{Q}=\mathbf{Q}\mathbf{Q}^T=1\tag{16}$$

这里，$det(\mathbf{Q})=1,and\ \mathbf{Q}^{-1}=\mathbf{Q}^T$，这里$\mathbf{1}$是一个$3\times3$的单位矩阵。如果需要求出坐标系$F$相对于坐标系$M$的旋转矩阵$\mathbf{Q}^\prime$，可以得到$\mathbf{Q}^\prime=\mathbf{Q}^T$，另外，我们从公式(13)中$\mathbf{Q}$矩阵的第一个元素$\mathbf{Q}_{1,1}$能够发现它是向量$\mathbf{u}$和$\mathbf{x}$的夹角余弦值，即$\mathbf{u}^T\mathbf{x}$。同样的结论对于其他各元素也成立。因此，这个旋转矩阵$\mathbf{Q}$就是直接余弦表示的旋转矩阵。这种表示法需要$3\times3$矩阵的9个参数，但是，9各参数并不是独立的，需要满足公式（14）的6个条件，因此，只有3个参数是独立的，这足以定义3个旋转自由度了。然后，这3个参数的选择是困难的，这也是直接余弦表达法的缺点。

2.Fixed-axes rotations

 Roll, Pitch and Yaw:围绕固定的X、Y和Z轴旋转也称为滚动、俯仰和偏航角度。这个命名法是常用于航空工程。绕着固定的惯性坐标系$F$旋转来表达运动坐标系$M$的方向，使用3个角度来表达旋转这种方式比较简单，在概念上类似于沿固定坐标系$F$的3个平移变换。坐标系$M$相对于坐标系$F$的方向由固定坐标系的3个基本旋转获得，如下图2所示。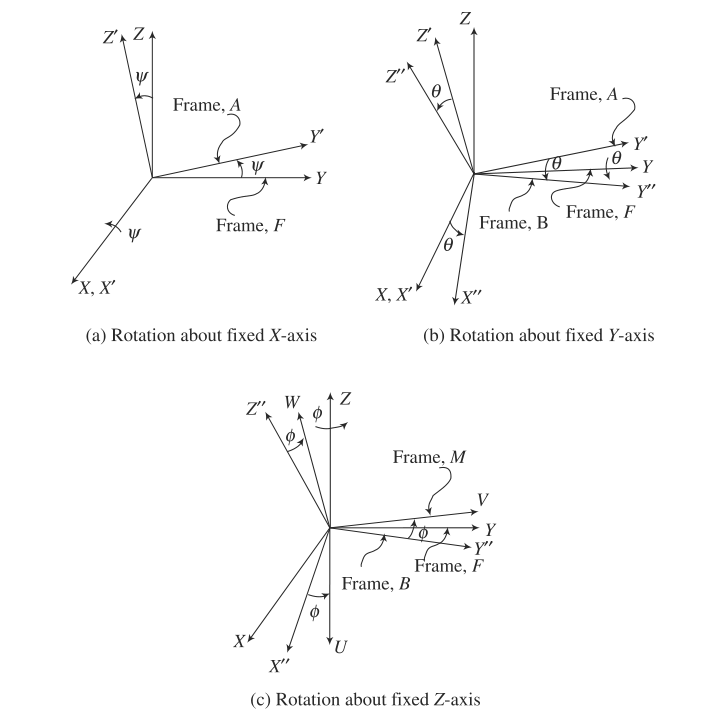

绕XYZ轴的旋转组合

 对于绕固定X、Y和Z轴的旋转，可以通过一系列基本旋转从固定坐标系F到达坐标系M，如图2所示。另$\psi,\theta\ and \ \phi$分别为绕$X-,Y-\ and \ Z-$轴的转角，总的旋转可以表达为基本旋转的组合：

• 绕固定坐标系$F$的$X$轴旋转的角度为$\psi$，如图2(a)所示，这个旋转用旋转矩阵$\mathbf{Q}_X$表示： $$\mathbf{Q}_X\equiv\left[ \begin{matrix}1&0&0\\0&C\psi&-S\psi\\0&S\psi&C\psi\end{matrix}\right]\tag{17}$$
• 从当前坐标系$A$绕坐标轴$Y$旋转一个角度$\theta$，如图2(b)所示，这个旋转矩阵用$\mathbf{Q}_Y$表示： $$\mathbf{Q}_Y\equiv\left[ \begin{matrix}C\theta&0&S\theta\\0&1&0\\-S\theta&0&C\theta\end{matrix}\right]\tag{18}$$
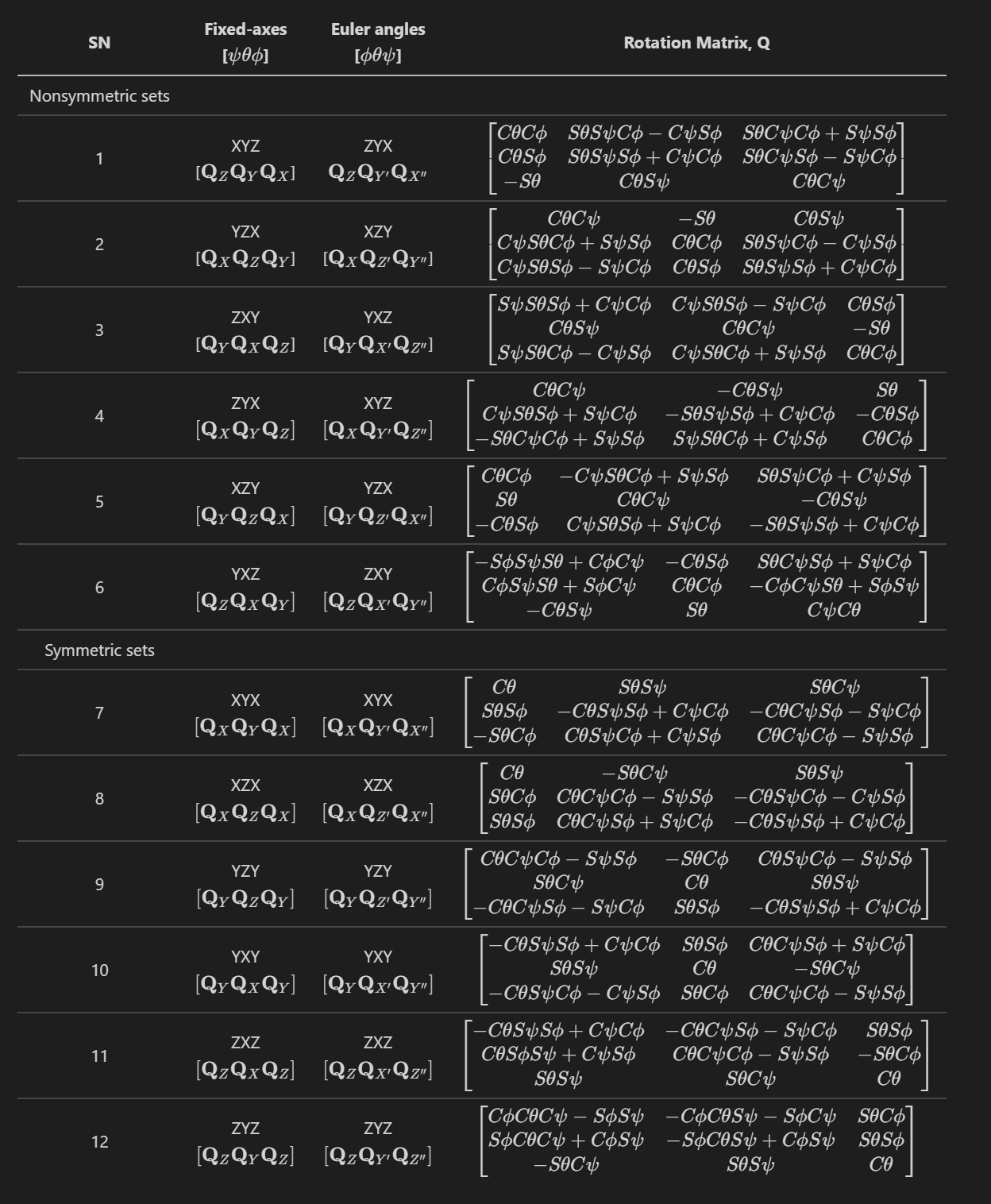
• 从当前坐标系$B$绕$Z$轴旋转一个角度$\phi$，如图2(c)所示，这个旋转矩阵用$\mathbf{Q}_Z$表示： $$\mathbf{Q}_Z\equiv\left[ \begin{matrix}C\phi&-S\phi&0\\S\phi&C\phi&0\\0&0&1\end{matrix}\right]\tag{19}$$  坐标系$F$的方向由矩阵$\mathbf{Q}$表示，方向矩阵$\mathbf{Q}$由基本旋转矩阵相乘得到： $$\mathbf{Q}=\mathbf{Q}_Z\mathbf{Q}_Y\mathbf{Q}_X\tag{20}$$ 详细结果如下所示： $$\mathbf{Q}=\left[ \begin{matrix}C\theta C\phi&S\theta S\psi C\phi-C\psi S\phi&S\theta C\psi C\phi+S\psi S\phi\\ C\theta S\phi&S\theta S\psi S\phi+C\psi C\phi&S\theta C\psi S\phi-S\psi C\phi\\-S\theta&C\theta S\psi&C\theta C\psi\end{matrix}\right]\tag{21}$$ 由于基本旋转不满足交换律，因此它们顺序的任何变化都会导致整体旋转矩阵$\mathbf{Q}$的不同，因此我们可以总结出12中组合，如表1所示。

3.Euler-angles representation

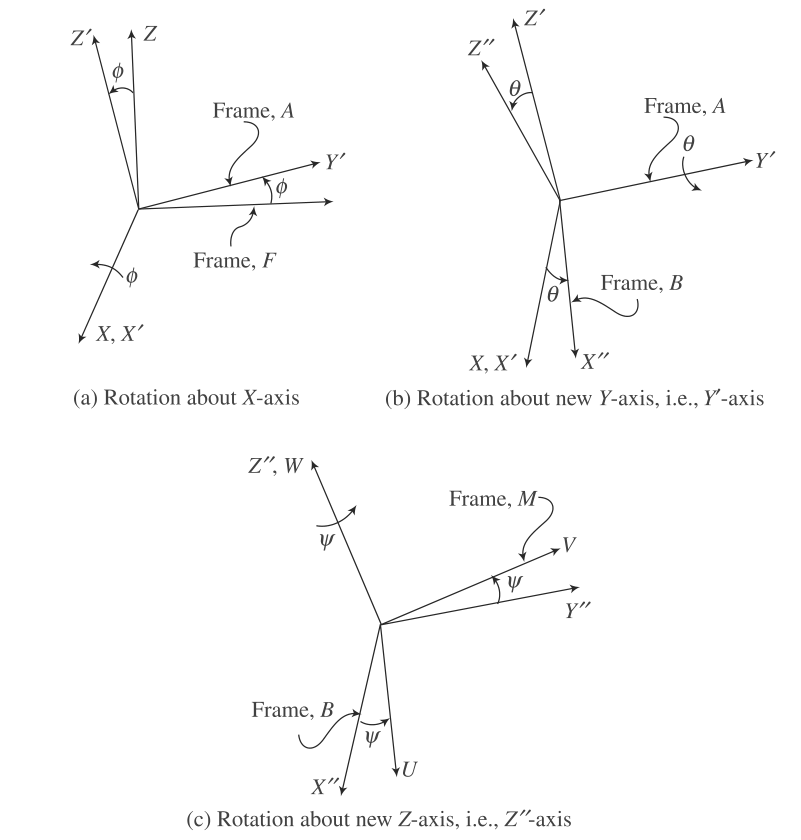
 欧拉角的表示法通过组合绕当前坐标系轴旋转的基本旋转来获得，不像固定轴旋转，这里的旋转是针对当前坐标。如图3所示。如果坐标系$F$先绕$X$轴旋转，再绕$Y^\prime$，最后绕$X^{\prime \prime}$轴旋转，最后的旋转矩阵$\mathbf{Q}$可以通过组合三个绕当前坐标系的基本旋转获得，分别是$\mathbf{Q}_X,\mathbf{Q}_{Y^\prime}$和$\mathbf{Q}_{Z^{\prime \prime}}$，得到：

$$\mathbf{Q} = \mathbf{Q}_X \mathbf{Q}_{Y^\prime} \mathbf{Q}_{Z^{\prime \prime}}\tag{22}$$

ZYZ欧拉角组合

 尽管已经有12个欧拉角组合存在，但是$ZYZ$组合也是最常用的表示法之一，如图4所示。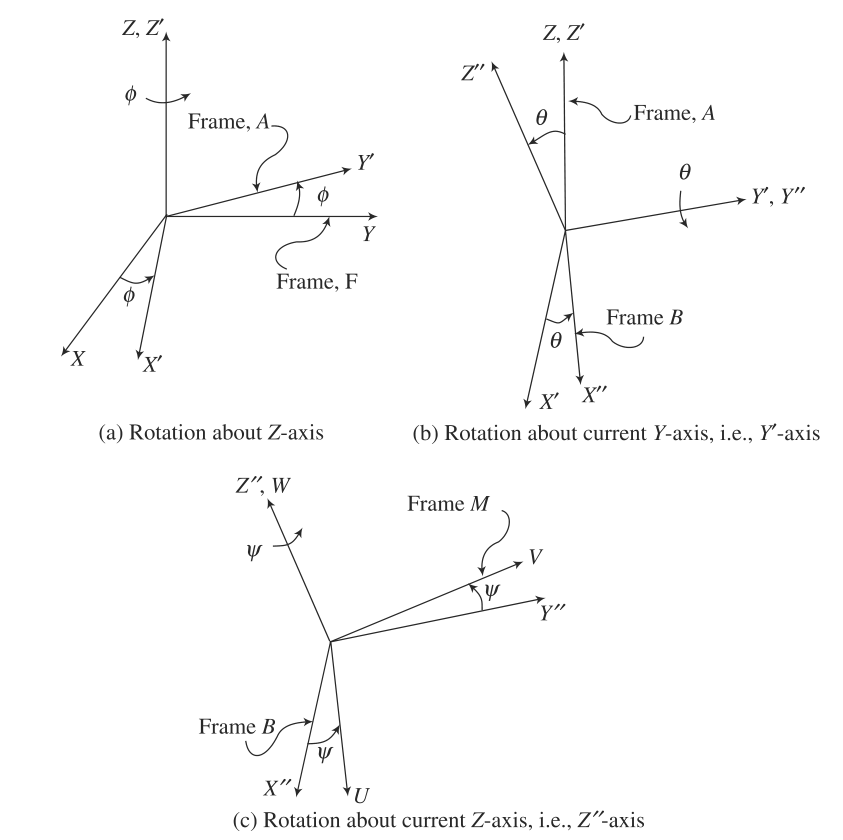

• 绕固定坐标系$F$的坐标轴$Z$旋转角度$\phi$，如图4（a）所示，这个旋转用旋转矩阵$\mathbf{Q}_Z$表示： $$\mathbf{Q}_Z \equiv \left[ \begin{matrix} C\phi&-S\phi&0\\S\phi&C\phi&0\\ 0&0&1\end{matrix}\right] \tag{23}$$
• 绕当前坐标系$A$的$Y^\prime$轴旋转角度$\theta$，用旋转矩阵$\mathbf{Q}_{Y^\prime}$表示，如图4（b）所示： $$\mathbf{Q}_{Y^\prime} \equiv \left[ \begin{matrix} C\theta&0&S\theta\\ 0&1&0\\ -S\theta&0&C\theta\end{matrix}\right] \tag{24}$$
• 绕当前坐标系$B$的$Z^{\prime \prime}$轴旋转角度$\psi$，如图4（c）所示，用矩阵$\mathbf{Q}_{Z^{\prime \prime}}$表示： $$\mathbf{Q}_{Z^{\prime \prime}} \equiv \left[ \begin{matrix}C\psi&-S\psi&0\\ S\psi&C\psi&0\\0&0&1 \end{matrix}\right] \tag{25}$$  最后坐标系$M$的方向矩阵$\mathbf{Q}$可以通过组合三个基本的旋转矩阵$\mathbf{Q}_Z,\mathbf{Q}_{Y^\prime} \ and\ \mathbf{Q}_{Z^{\prime \prime}}$获得： $$\mathbf{Q}=\mathbf{Q}_Z \mathbf{Q}_{Y^\prime} \mathbf{Q}_{Z^{\prime \prime}} \tag{26}$$ \mathbf{Q}矩阵的每个元素计算方式如下： $$\mathbf{Q}\equiv \left[ \begin{matrix}C\phi C\theta C\psi-S\phi S\psi&-C\phi C\theta S\psi-S\phi C\psi&S\theta C\phi\\ S\phi C\theta C\psi+C\phi S\psi&-S\phi C\theta S\psi+C\phi C\psi&S\theta S\phi\\ -S\theta C\psi&S\theta S\psi&C\theta \end{matrix}\right] \tag{27}$$

  4.Single- and double-axes rotations