基于波纹的地图分割MAORIS

一种利用自由空间布局分割不同模态地图的方法：MAORIS：基于波纹分割的地图

摘要

如何将楼层平面图或导航地图分割为语义表示，如房间和走廊，是研究人机交互、场所分类或语义地图等领域中一个重要的研究问题。虽然大多数工作集中在分割机器人创建的地图上，但这并不是机器人或其用户可以使用的唯一地图类型。我们提出了一种分割不同模态地图的方法，重点是机器人创建的地图和手绘草图地图，并展示了比最先进技术更好的结果。

我们的方法通过对地图的距离图像和一个圆形卷积核进行卷积，并将相同值的像素分组来分割地图。通过检测像波纹般的模式，其中像素值迅速变化，并合并具有类似值的相邻区域来完成分割。

我们确定了最近工作中使用的分割评估度量中的缺陷，并提出了一种基于马修斯相关系数（MCC）的度量。我们将我们的结果与公开可用数据集中地图的真实分割进行比较，我们获得了比最先进的分割方法更好的MCC值，与最近一种基于Voronoi分割方法的0.65相比，我们的结果为0.98，DuDe分割方法的MCC值为0.70。我们还提供了一个室内环境手绘图的数据集，有两组可能的真实分割结果，我们的方法在这个数据集上获得了0.56的MCC值，而基于Voronoi分割的方法和DuDe分割方法的MCC值分别为0.28和0.30。

I. 引言

目前最先进的SLAM算法使得机器人能够构建代表其环境的度量地图。然而，机器人构建的地图（称为机器人地图）并不总是易于理解。它们受到传感器噪声、杂乱无章的影响，并且如果环境庞大而复杂，它们可能会变得复杂。对于人类来说，使用高级特征（例如房间和走廊）通常比直接呈现机器人地图更容易理解。这在人与机器人交互等领域是正确的，人们可以使用房间名称而不是坐标来沟通位置和方向，在规划中也是如此，机器人需要以最佳顺序访问房间。

但机器人地图不是机器人可以使用的唯一类型的地图。例如，手绘草图是人机交互非常直观的界面，能够有效传达空间配置，正如Skubic等人所示[1]。然而，草图地图在度量上不准确，有时是故意的。例如，绘制者可能会完全忽略环境中的某个特征，因为他们认为它不重要。虽然人类能够考虑到这些变化，并理解图纸中的抽象，但机器人却很难解释这种模糊的环境表示。

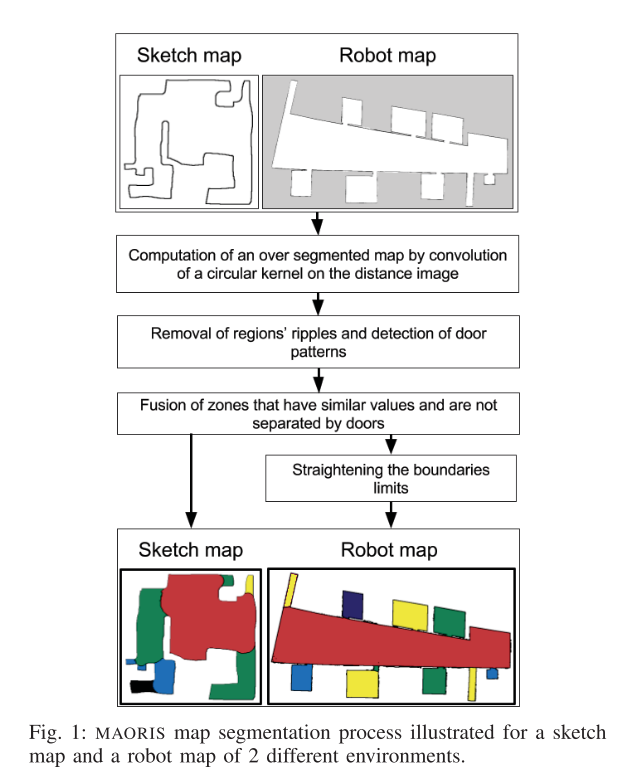
在我们的工作中，我们提出了一种新颖的地图分割方法，即使来自非常不同的模态，也能够应用并聚焦于机器人和草图地图。本文提出了一种从不同模态的地图中提取区域的新方法（如图1所示）。该算法在代表机器人地图和手绘地图的数据集上进行了评估，并与用户提供的地面真实分割进行了比较。本文的贡献包括：

• 一种比现有技术更稳健的新型地图区域提取方法；
• 包含三个室内场所的手绘地图数据集，并且所有区域均由人工标注分割；
• 一种讨论如何评估和比较地图分割算法结果的方法，以及一种新的度量方法。

II. 相关工作

Bormann et al.[2] 对房间分割的文献进行了综述，并选择并实现了四种算法作为ROS包。他们使用20个楼层平面图来提供和比较这些方法；在大多数情况下，基于Voronoi图的分割给出了最接近实际分割的结果。然而，基于Voronoi图的分割往往对区域进行过度分割，特别是走廊。此外，草图地图的噪声特性使得提取Voronoi的主要骨架变得困难，导致过度或不足分割。

Fermin-Leon等人[3]提出了DuDe分割方法，该方法利用基于轮廓的部分分割[4]构建2D拓扑地图。他们开发了批处理和增量算法进行分割，并将其与Bormann等人[2]提出的方法进行了测试。虽然基于Voronoi图的分割表现更好，但他们的方法更快。然而，他们的方法对走廊进行了过度分割。此外，它基于轮廓形状，在对细节关注较少的草图上使用时，会导致较差的分割结果，如第IV-C节所示。

Fabrizi等人[5]使用图像处理从声纳构建的占用格网中提取特征。他们使用模糊开操作和闭操作来计算有关自由空间的信息，并使用分水岭算法创建区域。根据区域的离心率，将区域分类为房间和走廊。分水岭算法使用门的模式来避免将不同的房间融合在一起。然而，并非所有地图上都存在这些门的模式。

Park等人[6]从地图中提取最大空矩形，并将其用于地图匹配。由于地图的方向、准确性和比例尺是未知的，最终合并的地图是通过最小化这些因素的差异来估计的。该方法依赖于地图中存在直角角度，这在草图地图中并不现实。

Ahmed等人[7]和Heras等人[8]讨论了一种使用具有符号和文本注释的建筑楼层平面图的系统。他们的方法适用于具有高准确性和大量细节的楼层平面图，例如不同类型的墙壁和标签，但不适用于草图和机器人地图。

Diosi等人[9]实现了一种半自主的房间分割算法。机器人在跟随用户的同时对环境进行地图绘制，并由用户为不同位置提供标签。完成地图绘制后，距离图像用于生成局部极大值，并使用梯度上升将所有移动到同一局部极大值的像素分组为区域。未标记的片段被合并到最小化未标记片段质心与最近标签之间距离的标记片段中。由于该方法依赖于用户的先前标注和标签在地图上的位置，因此对于草图和一般用例来说并不适用。

III. 地图分割

我们假设可以通过观察自由空间的布局来找到室内地图中的区域；更具体地说，通过观察房间之间的尺寸变化，例如房间之间的门或不同尺寸的房间和走廊。先前的工作，例如Bormann等人[2]的基于距离变换的分割，使用距离图像上的阈值来提取最大数量的区域。因此，找到合适的阈值取决于最大和最小区域之间的尺寸差异。此外，该阈值是由用户根据环境任意选择的。另一方面，我们的方法使用距离图像生成一个新的图像，其中像素的值表示其所属区域的大小。通过观察这个图像，我们的方法不依赖于区域的形状，只依赖于相邻区域之间的大小差异，这是比最大和最小区域之间的差异更相关的度量。

算法 1: 分割算法。

数据: 地图
结果: 分割后的地图

1. 从地图计算距离图像；
2. 计算自由空间图像；
3. 将相邻像素值相同的像素分组成区域；
4. 去除波纹；
5. 合并具有相似值且未被门隔开的区域；
6. 移除由厚墙创建的区域；
7. 如果地图是机器人地图，则执行以下步骤：
8. 修正边界；
9. 结束
10. 返回分割后的地图；

在本节中，我们介绍了用于地图分割的算法，即算法1。本节的其余部分将解释以下关键要素：A.从自由空间的布局中提取过度分割的地图，B.去除我们称之为波纹的特定类型的区域，C.通过合并具有相似值的邻域并检测门的模式（如果存在）进一步细化分割，D.和E.去除由厚墙创建的区域，并对机器人地图进行轮廓修正。

A. 计算自由空间图像

我们首先计算一幅图像，其中每个像素的值表示其所属区域的大小，称为自由空间图像（FSI）。实际上，FSI代表了图像中每个像素周围的自由空间的大小。

提取FSI的算法如算法2所示。它的开始是计算地图的距离图像，即每个像素的值表示到最近障碍物的距离。对于距离图像的每个像素，我们创建以该像素为中心、半径为像素值的圆形掩膜。对于圆形掩膜中的每个像素，如果相应FSI中的像素值小于圆形半径，则FSI像素的值被更改为圆形半径。处理完所有像素后，将具有相同值的相邻FSI像素分组成区域。

算法2: 提取自由空间图像 (FSI)
输入: 地图图像
输出: 自由空间图像 (FSI)

1. 计算地图的距离图像

2. 使用与地图图像相同尺寸的图像初始化FSI图像，所有像素值设为0

3. 对于距离图像中的每个像素(x, y):

- 设r为距离图像中像素(x, y)的值
- 创建以像素(x, y)为中心、半径为r的圆形掩膜
对于圆形掩膜中的每个像素(u, v):
- 如果FSI中相应的像素值FSI(u, v) < r，则更新FSI(u, v) = r

4. 将具有相同值的相邻FSI像素分组成区域

5. 返回自由空间图像 (FSI)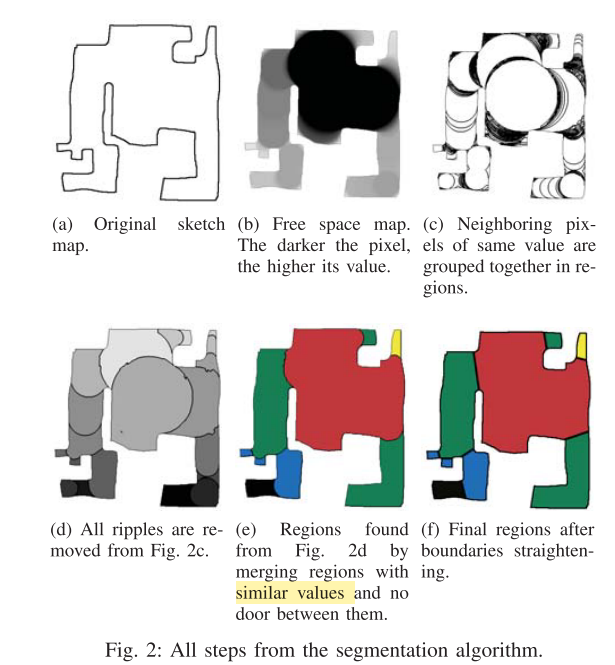

由于我们对地图中的区域没有假设任何特定方向，我们使用了一个圆形掩膜，但其他形状也可以用于其他应用，例如，对于只有直角角度的环境，可以使用正方形形状。示意图2b展示了示意图的FSI的示例。

B.波纹区域的合并

FSI提供了一个过分割的地图，即使是微小的区别也会被表示出来（见图2c）。像素值上的微小变化会产生波纹，即极细的区域，其像素值略有变化。这些通常存在于较大区域之间，算法的第二步通过将它们合并到更大的区域中来消除波纹。

但是，重要的是将波纹合并到它们所属的区域中。否则，两个波纹可能会合并在一起，造成不该有任何波纹的区域中出现了波纹，使地图过分割。由于波纹比它们所属的区域小，因此通过从像素值最高的区域到最低的区域考虑区域，算法首先将大波纹合并到大区域中，然后将较小的波纹合并到剩余的区域中，从而避免过度分割。

仅需要一个简单的规则来检测波纹。由于波纹是被拉伸的，因此其周围约有一半的轮廓与相邻区域接触，即邻居区域。如果一个区域的轮廓超过40%与邻居区域接触，则该区域将与其邻居区域合并。如果一个区域是多个区域的波纹，则它将与像素值最接近的区域合并。每当合并波纹时，都会再次检查波纹的所有相邻区域，以查看它们是否变成了新合并的区域的波纹。在第IV-A节中，展示了稳定性分析，证明使用40%可以得到良好的地图分割。在波纹合并后，可以在图2d中看到示意图的分割结果。

C. 合并具有相似像素值的邻近区域。

此时，地图分割仍然具有属于同一位置但不是涟漪的区域需要合并，例如：逐渐变小的走廊将被分成不同大小的多个部分。如图2d所示，左侧的走廊仍然分成多个区域，因为其宽度不一致。因此，算法的这一步将合并具有相似像素值的相邻区域。

我们定义pV1和pV2为两个区域的像素值，t_mergin是合并阈值，m是添加到合并阈值的边距。t_mergin是介于0和1之间的数字，表示自动合并的相对像素值差异，其中0表示无法合并，1表示总是合并区域。因此，合并阈值和边距表示需要先考虑两个区域的相似度。我们从包含最多像素的区域到包含最少像素的区域进行分类，并递归地查看所有相邻区域。如果值差异|pV1-pV2|小于最高像素值乘以阈值，即公式（1）成立，则合并两个区域。

$$|pV1-pV2| < max(pV1,pV2)*t\_mergin (1)$$

然而，使用固定的阈值并不能合并所有应该合并的区域，因为区域的模糊性质。因此，对于相邻的两个区域，如果|pV1−pV2| 超过了最高像素值与阈值相乘的结果，即不满足公式(1)，但它却小于加上幅值m后的同一公式，即公式(2)成立，算法将检查这些区域的邻域以确定它们是否应该合并。只有当两个区域中的某一个区域具有与另一个区域的至少一个邻居类似的像素值时（即公式(1)在一个区域与另一个区域的至少一个邻居之间成立）时，算法才会合并这些区域。

$$|pV1-pV2| < max(pV1,pV2)*(t\_mergin+m) (2)$$

当存在波纹的区域时，如果波纹是由门造成的，则该算法不会考虑这些区域是否需要合并。可以通过查看两个区域之间存在的所有波纹的最小值来找到门，并确保这个最小值与两个区域之间的像素值差异不显著，即不满足条件(1)。

在t_merging和m的稳定性分析可参见第四部分-A。图2a的最终分割版本可参见图2e。

D.考虑墙壁厚度

厚墙可以通过创建小区域来过度分割地图，例如，有门的地方。算法不是假设我们知道墙的厚度，而是认为每个与其他区域接触的周长超过一定百分比d_threshold的区域属于另一个区域。因此，这些区域将与接触其他区域周长小于d_threshold的相邻区域融合在一起。该参数的稳定性分析可以在第IV-A节中找到。

E. 边界直线化

区域之间的接触线取决于第III-A节中使用的掩模的形状。圆形掩模适用于草图地图，因为绘制不准确，区域之间的边界可能不是直线。然而，对于度量正确的机器人地图，可以将区域之间的边界直线化以提高分割的准确性。我们用端点之间的直线替换每个区域之间的边界。

虽然这一细化步骤不适用于草图地图，但为了说明目的，在图2a的直线分割版本中可以看到通过直线化的边界（如图2f所示）。

IV. 实验

我们将我们的方法与Bormann等人[2]提出的方法以及Fermin-Leon等人[3]的DuDe方法进行了比较，并使用了Bormann等人[2]的数据集和我们自己的草图数据集[10]。Bormann等人[2]的数据集包含20个地图，其中有些没有杂物，有些则人为添加了杂物。由于我们的方法仅适用于没有家具的环境，我们使用了没有杂物的图像。杂物可以通过预处理步骤或提取环境的墙壁来去除，就像Wulf等人[11]所做的那样；我们将这些想法留给未来的工作。

我们提供了一个包含25个草图的数据集。这些草图是从一个网页浏览器中的虚拟环境中获得的，并对应于KTH SLAM数据集的地面真实数据（图4）。每个草图地图都与两种可能的地面真实分割相关联，这是通过要求两个非专家用户对草图进行分割获得的。唯一的指示是对区域进行分割，以便如果一个机器人或人需要访问该环境，他们可以通过访问地图的每个区域来看到环境的每个部分。

Bormann等人[2]提出了一个基于精确率和召回率的质量度量方法，其中，分割区域的精确率是分割区域与地面真实区域的最大重叠面积与分割区域面积的比值，而地面真实区域的召回率是地面真实区域与分割区域的最大重叠面积与地面真实区域面积的比值。完整分割的精确率是所有分割区域精确率的平均值，而召回率是所有地面真实区域召回率的平均值。如果精确率和召回率都较高，则分割结果是好的。

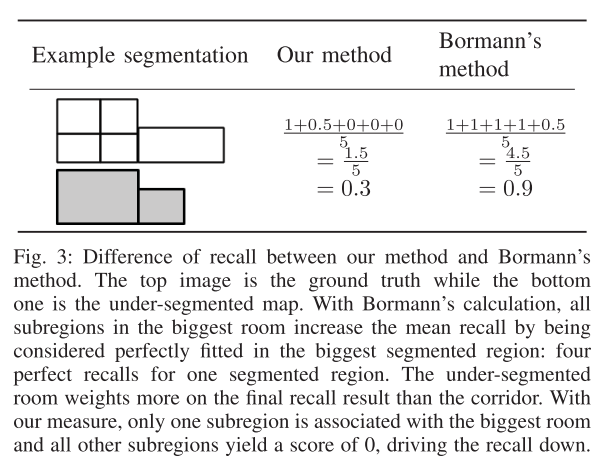
尽管这个度量指标评估了分割结果与地面真实数据的匹配程度，但它对于欠分割的情况倾向于产生高召回率的结果，并且对于过分割的情况倾向于产生高精确率的结果，正如图3中召回率所示。实际上，分割的召回率是所有地面真实区域召回率的平均值，如果一个分割区域包含多个地面真实区域，它将在分割的召回率上占据很大的权重。在某些情况下，它几乎可以抹消分割区域的影响，就像图3中的情况，其中中央房间的召回率超过了走廊的召回率。类似的情况也适用于精确率。

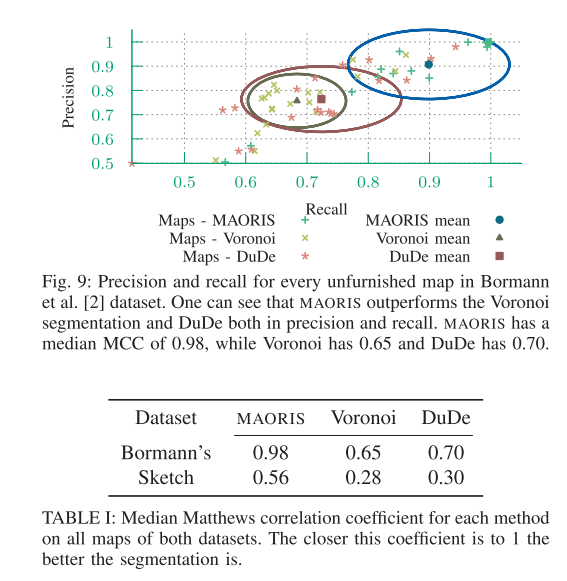
此外，由于精确率和召回率的计算中真正阳性值（同时适用于地面真实区域和分割区域的像素）并不相同，这些度量指标使我们无法表示混淆矩阵或计算有意义的指标，例如F值、G值或马修斯相关系数。

我们引入了另一种评估分割结果的方法，借鉴了聚类度量的思想。每个分割区域与具有最大重叠但尚未与分割区域关联的地面真实区域相关联。真正阳性（tp）是分割区域和地面真实区域中的所有像素，假正例（fp）是分割区域中的像素但不在地面真实区域中，假阴性（fn）是地面真实区域中的所有像素但不在分割区域中，真负例（tn）是既不在地面真实区域中也不在分割区域中的所有像素。为了能够比较每个分割算法给出的不同结果，我们使用马修斯相关系数（MCC）进行评估：

$$MCC = \frac{tp*tn-fp*fn}{\sqrt{(tp+fp)(tp+fn)(tn+fp)(tn+fn)}} (3)$$

马修斯相关系数（MCC）的取值范围在-1到1之间，最好的预测结果为1，0表示与猜测没有区别，-1表示完全不一致。评估地图分割时，MCC的一个优点是即使类别的大小不同，它仍然保持平衡。虽然没有一种单一数字可以最好地表示混淆矩阵，但MCC通常被认为是最好的度量指标之一[12]。未与对应区域关联的区域的MCC为0。分割地图的最终MCC是所有区域的MCC的平均值。评估程序的公开实现可以在MAORIS软件包的在线版本中找到。

A. 参数稳定性评估

我们使用中位数MCC作为衡量分割效果的指标，对我们方法的每个参数进行了稳定性分析。我们对Bormann数据集中最小的16张无杂物的地图以及我们的手绘地图数据集中的所有地图进行了分析，并与其中一个用户的地图真值分割进行了对比。

我们首先确认了使用40%作为判断区域是否为波纹的阈值是一个有效的假设。如图5所示，MCC在30%至45%之间达到最佳值，最高值出现在40%，这证实了阈值的有效性。

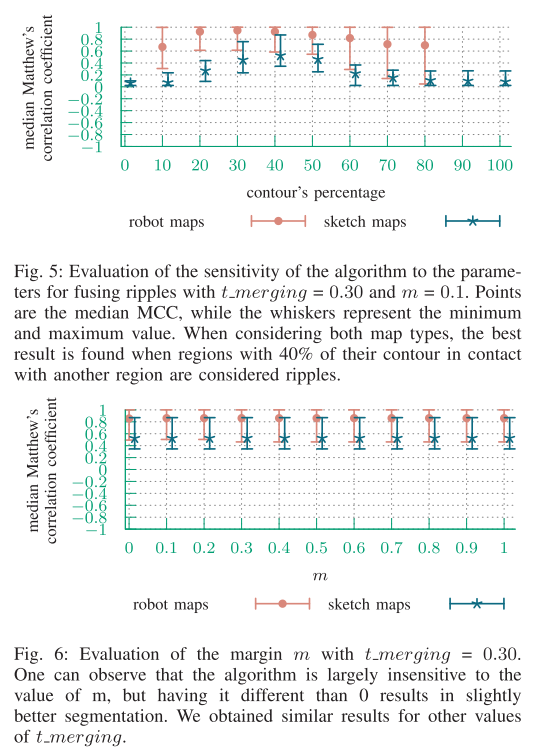
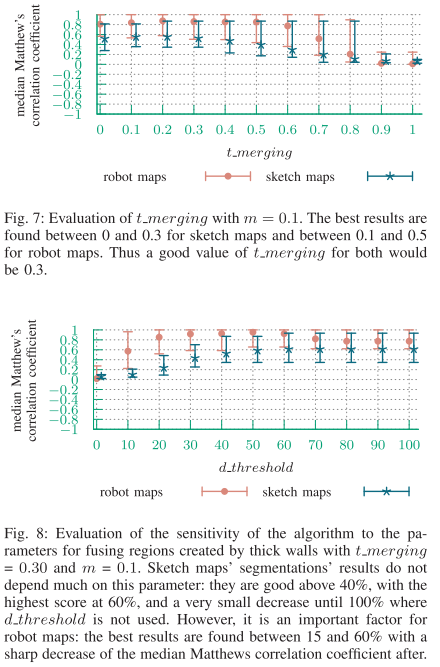
然后我们评估了对于合并阈值t_merging和边界值m的分割结果的稳定性。从图6中可以看出，对于边界值m，算法对其值并不敏感，因为它对于草图地图的分割没有影响，并且只在不等于0时稍微提高了机器人地图分割的MCC值。在我们的工作中，我们选择了m=0.1。对于合并阈值t_merging的分析结果可以见于图7。可以看出，随着t_merging的增加，分割效果会提高，但在达到一定点后会下降：机器人地图中约为t_merging=0.5，草图地图中约为t_merging=0.3。此外，需要注意的是，在t_merging=0.2和0.4之间，机器人地图的MCC值保持不变。草图地图和机器人地图之间的这些不同值来自于机器人地图中不同区域之间存在的门。门在区域之间创建了分隔，即使它们的大小相似，也可以允许更高的合并阈值，而不会合并不应该合并的区域。然而，我们数据集中的草图地图没有门，导致在t_merging=0.3以上的中位数MCC值较低。为了获得良好的结果，我们选择了t_merging=0.3。因此，当两个区域的大小差异超过最大区域大小的1/3时，它们不会被合并在一起。

最后，我们评估了d_threshold参数对分割结果的影响。从图8中可以看出，草图地图的分割对该参数并不敏感：草图地图的中位数MCC在40%以上是良好的，其值在60%之后略微下降，直到100%。我们推测用户在绘制时考虑了笔的大小，因此没有通过墙体厚度创建区域。另一方面，对于机器人地图来说，d_threshold是一个重要的参数：最佳结果在30%和60%之间，且在100%之前保持正确。对于不确定是否需要考虑墙体厚度的应用程序，我们建议将40%作为最佳选择。在我们的工作中，我们选择了机器人地图的d_threshold为40%，草图地图的d_threshold为60%。

B. Bormann数据集上的分割结果

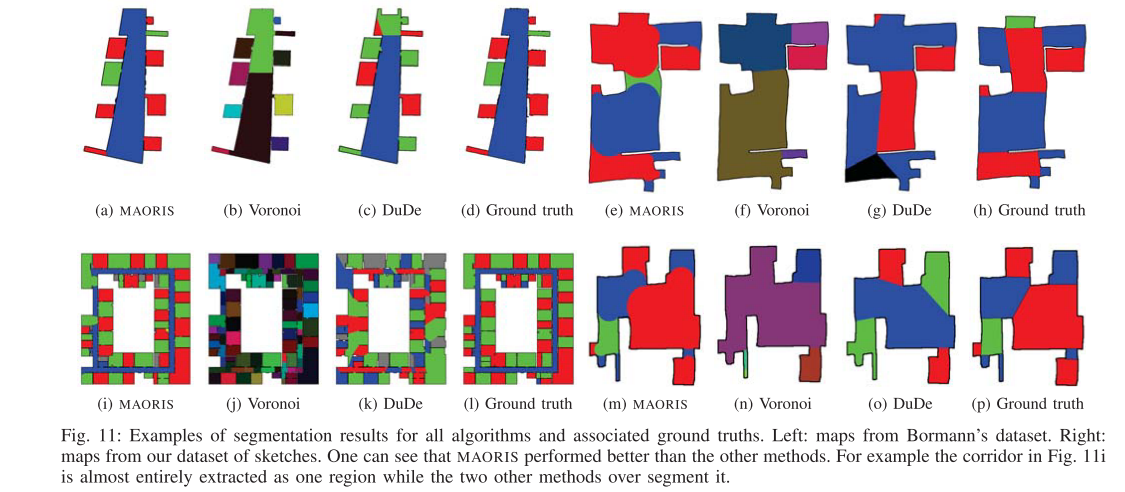
我们在Bormann等人提供的20个无杂乱地图上运行了我们的算法（MAORIS）。每张地图的精确度和召回率结果如图9所示，MCC结果如表I所示。Bormann等人基于Voronoi的分割方法获得了0.65的MCC值，而Fermin-Leon等人的DuDe方法获得了0.70的MCC值。相比之下，我们的方法的中位数MCC为0.98，因此表现优于其他两种方法。Bormann数据集中的地图示例上，三种算法的分割结果如图11所示。

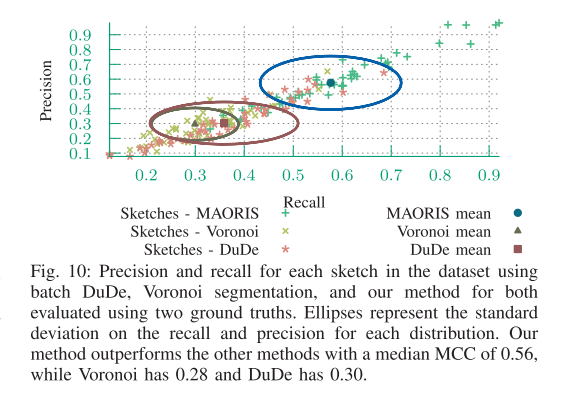
在我们的25个手绘地图数据集上，我们对三种算法进行了运行，并提供了两个用户提供的地面真实分割结果。MAORIS在分割手绘地图方面表现更好，MCC为0.56，而Voronoi分割的MCC为0.28，DuDe方法的MCC为0.30。从图10可以看出，Voronoi分割和DuDe方法具有较高的精度但较低的召回率。另一方面，MAORIS在精确率和召回率之间具有更好的平衡。

考虑到我们的数据集中的草图地图没有门，值得注意的是，MAORIS的MCC为0.56，不依赖于区域之间的门进行分割，这与先前的工作[5]不同。图11展示了三种算法在我们的草图数据集上的分割示例。

第五部分 限制与未来工作

MAORIS的速度取决于图像的大小。由于该方法是基于像素的，图像中的像素越多，方法的速度就越慢。这个缺点可以通过降低大型图像的分辨率来轻松克服。在Bormann等人的数据集上，当在Intel i7-4712HQ 2.30GHz、16GB RAM的计算机上运行时，MAORIS的平均处理时间为43秒。然而，大部分处理时间来自于2张大型地图。如果去除这两张地图，平均处理时间为8.8秒。在Bormann的数据集上，使用Intel Core i7 2.70GHz的CPU，DuDe方法在1秒内处理了95%的地图[3]，而Voronoi分割则大约需要13秒[2]。在草图数据集上，MAORIS的平均处理时间为6秒。开发一种增量式的MAORIS分割方法将提高处理速度，这将留待未来的工作。

另一种改进MAORIS的方式是能够处理地图中的杂物。在未来，我们计划研究在分割之前自动去除地图中的杂物的方法，从而使我们能够对杂乱的地图进行分割。我们还计划利用MAORIS分割方法提供的区域来在不同模态的地图之间进行匹配。

参考文献

[1] M. Skubic, D. Anderson, S. Blisard, D. Perzanowski, and A. Schultz, “Using a hand-drawn sketch to control a teamof robots,” Autonomous Robots , vol.22, no.4, pp.399–410,Mar.20, 2007, ISSN : 0929-5593, 1573-7527.DOI : 10.1007/s10514-007-9023-1.

[2] R. Bormann, F. Jordan, W. Li, J. Hampp, and M. H ¨agele, “Room segmentation: Survey, implementation, and analysis,” in IEEE International Conference on Robotics and Automation (ICRA) , IEEE, 2016, pp.1019–1026.

[3] L. Fermin-Leon, J. Neira, and J.A. Castellanos, “Incremental contour-based topological segmentation for robot exploration,” in IEEE International Conference on Robotics and Automation (ICRA) , May 2017, pp.2554–2561.DOI :10.1109/ICRA.2017.7989297.

[4] G. Liu, Z. Xi, and J.-M. Lien, “Dual-space decomposition of 2d complex shapes,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , 2014,pp.4154–4161.

[5] E. Fabrizi and A. Saffiotti, “Extracting topology-based maps from gridmaps,” in IEEE International Conference on Robotics and Automation (ICRA) , vol.3, IEEE, 2000,pp.2972–2978.

[6] J.Park, A. J. Sinclair, R. E. Sherrill, E. A. Doucette, and J. W. Curtis, “Map merging of rotated, corrupted, and different scale maps using rectangular features,” in 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS) , Apr.2016, pp.535–543.DOI : 10.1109/PLANS.2016.7479743.

[7] S. Ahmed, M. Liwicki, M. Weber, and A. Dengel, “Automatic room detection and room labeling from architectural floor plans,” in Document Analysis Systems (DAS), 2012 10th IAPR International Workshop on , IEEE, 2012, pp.339–343.

[8] L.-P .de las Heras, S. Ahmed, M. Liwicki, E. V alveny, and G. S ´anchez, “Statistical segmentation and structural recognition for floor plan interpretation: Notation invariant structural element recognition,” International Journal on Document Analysis and Recognition (IJDAR) , vol.17, no.3, pp.221–237, Sep. 2014, ISSN : 1433-2833, 1433-2825.DOI : 10.1007/s10032-013-0215-2.

[9] A. Diosi, G. Taylor, and L. Kleeman, “Interactive SLAM using laser and advanced sonar,” in IEEE International Conference on Robotics and Automation (ICRA) , IEEE, 2005,pp.1103–1108.

[10] M. Mielle, M. Magnusson, and A. J. Lilienthal, Sketch maps
dataset , Sep. 2017.DOI : 10.5281/zenodo.892062.

[11] O. Wulf, K. O. Arras, H. I. Christensen, and B. Wagner, “2d mapping of cluttered indoor environments by means of 3d perception,” in IEEE International Conference on Robotics and Automation (ICRA) , IEEE, vol.4, 2004, pp.4204–4209.

[12] D. M. Powers, “Evaluation: From precision, recall and fmeasure to ROC, informedness, markedness and correlation,” Tech.Rep., 2011.