基于网格的离线覆盖路径规划

摘要

在视频游戏中，全面覆盖的算法方法具有应用价值，可以实现自动游戏级别探索。当前的设计采用简单的启发式方法，经常导致性能不佳或展现出不自然的行为。在本文中，我们介绍了一种新的算法，用于覆盖一个2D多边形区域（带洞）。我们假设已知地图布局，并使用基于网格的世界表示。在多个场景上进行的实验分析，从简单布局到实际游戏中使用的更复杂地图，都表现出良好的性能。这项工作是构建更有效的覆盖路径规划算法的初始步骤，以用于非玩家角色。

1 简介

覆盖路径规划(CPP)是指规划一个代理器在跨越一个特定区域时遍历所有区域的路径。此问题中最具挑战性的一个方面是优化代理器的规划路径，使其覆盖感兴趣的区域[1]。CPP可分为两种类型: 离线或在线[2]。在离线覆盖中，代理器已知环境布局，而在线覆盖则是代理器没有环境先验知识。此问题可通过多种方法解决。在本文中，我们使用基于网格的方法实现一种新的算法来覆盖感兴趣的区域。我们的算法易于实现，但也可以保证解决任何区域兴趣的问题。该算法不能保证最优解，但提供了将覆盖扩展到多个代理器而不需要额外复杂性的基础。在接下来的一节中，我们将介绍与覆盖路径规划领域相关的工作，然后描述我们工作的方法论。接着，我们将描述算法在选择的场景中所取得的结果。最后，我们将得出结论和未来的工作。

2 相关工作

覆盖路径规划在机器人领域已经得到充分研究，用于各种应用程序，比如吸尘器机器人[3]，割草机[4]，无人机（UAV）监控[5]等。文献中包含了几种CPP方法，但是方法很大程度上取决于空间的表示方式，要么依赖于连续空间表示，如凸包形式，要么依赖于离散的基于网格的模型。

通过凸包分解将可通过的空间划分为简单的不重叠的凸多边形区域。在分解之后，解决覆盖路径规划问题依赖于找到访问这些区域的最短路径，以及每个区域的覆盖模式。适当的覆盖模式示例如锯齿形[6]，螺旋形[7]。一旦空间被分解成凸子区域，可以使用一个相邻图来表示分解空间。在图中，节点是凸区域，节点之间的边表示凸区域之间的相邻关系。智能体使用这个图来规划最短路径以遍历所有凸子区域，递归地为每个区域规划最短覆盖模式。

基于网格的方法将空间分解为均匀分布的节点网格[8]，每个节点可以是可遍历或不可遍历的。在这种表示中，通过遍历所有可达节点来完成CPP，与覆盖相关的属性可以是二进制或概率性的[9]。基于网格的方法取决于网格的粒度，因此其完备性取决于网格的细度。基于网格的表示是使用最简单的方法之一。但是，对于较大的空间，与其他方法相比，这种方法的计算成本变得非常昂贵[10]。

3 方法

本节中，我们介绍了我们算法选择的空间表示方法。接着，我们将解释我们的算法如何完成覆盖路径规划到一个感兴趣的区域。

3.1 空间表示

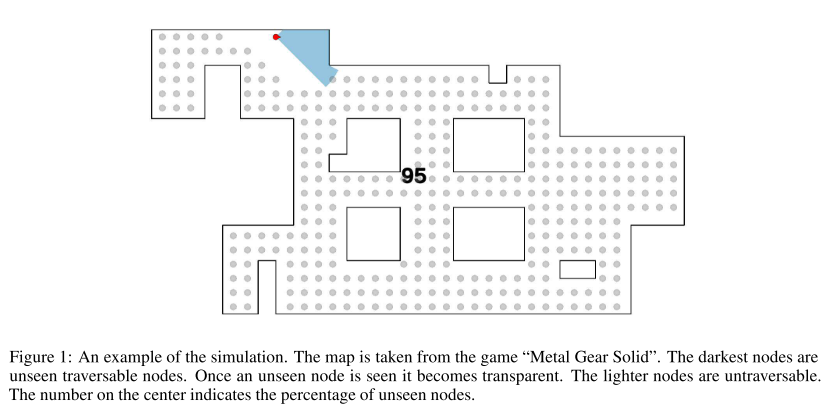
对于我们的方法，我们使用了基于2D网格的表示方法；将空间离散化成网格节点，每个节点有三种可能的状态：不可通过、已看到和未看到。网格连通性基于von Neumann邻域，代理通过在四个方向上取一个步长来移动；上、下、左、右。代理视野的表示由一个有限范围和角度的锥形表示；其他视野模型也可以。当未看节点落在视野锥体内时，该节点变为已看到。如果所有可通行的节点都被看到，则考虑该场景已成功完成的条件已达成。图1为该模拟的示例。
图1：模拟实例。地图取自游戏“合金装备空降行动”。最暗的节点是未看到的可通行节点。
一旦一个不可见节点被看到，它就变得透明。较浅的节点是不可穿过的。中央的数字表示未见节点的百分比。

3.2 波前算法

针对我们的方法，我们基于 WaveFront 覆盖算法实现 [11]。我们将其称之为“波前算法”。该算法通过将来自未见节点的距离通过已见节点进行传播来工作。传播过程每隔固定的时间间隔就会被执行一次。算法 1 显示了波纹前缘的伪代码，其中 N 是网格中节点列表，D(n) 是到最近未见节点的曼哈顿距离。在每次迭代中，通过将 Min(D(l)) 赋值给 D(n) 来更新 D(n)。D(n) 值将通过添加 D(ni)+1 来更新，其中 ni 是与最近未见节点之间的最短距离的相邻节点。添加的 1 表示从 n 到 ni 的步骤成本。

波纹前沿算法的重点是创建一个总体道路图，使得代理可以轻松决定下一步朝哪个方向前进以发现未见过的位置。然而，由于代理人采取的是贪婪的决策过程，即简单地面对并朝向距离未见节点最近的节点，因此覆盖路径不能保证最优。尽管如此，此方法提供了解决地图的保证。

参考文献

[1] Chung-Hsien Kuo, Hung-Chyun Chou, and Sheng-Yu Tasi.Pneumatic sensor: A complete coverage improvement approach for robotic cleaners.IEEE Transactions on Instrumentation and Measurement , 60(4):1237–1256,2011.

[2] Howie Choset.Coverage for robotics–a survey of recent r esults.
Annals of mathematics and artificial intelligence ,31(1-4):113–126, 2001.

[3] Fumio Yasutomi, Makoto Yamada, and Kazuyoshi Tsukamoto .Cleaning robot control.In Proceedings.1988 IEEE International Conference on Robotics and Automation , pages 1839–1841.IEEE, 1988.

[4] Zuo Llang Cao, Yuyu Huang, and Ernest L Hall.Region fillin g operations with random obstacle avoidance for mobile robots.Journal of Robotic systems , 5(2):87–102, 1988.

[5] Nicola Basilico and Stefano Carpin.Deploying teams of h eterogeneous uavs in cooperative two-level surveillance missions.In 2015 IEEE/RSJ International Conference on Intelligent Rob ots and Systems (IROS) , pages
610–615.IEEE, 2015.

[6] Howie Choset and Philippe Pignon.Coverage path plannin g: The boustrophedon cellular decomposition.InField and service robotics , pages 203–209.Springer, 1998.

[7] Fotios Balampanis, Ivan Maza, and Anibal Ollero.
Spiral -like coverage path planning for multiple heterogeneous
uas operating in coastal regions.
In 2017 International Conference on Unmanned Aircraft System s (ICUAS) ,
pages 617–624.
IEEE, 2017.

[8] Hans Moravec and Alberto Elfes.High resolution maps fro m wide angle sonar.In Proceedings.1985 IEEE International Conference on Robotics and Automation , volume 2, pages 116–121. IEEE, 1985.

[9] Alberto Elfes.Sonar-based real-world mapping and navi gation.IEEE Journal on Robotics and Automation ,3(3):249–265, 1987.

[10] Sebastian Thrun.Learning metric-topological maps fo r indoor mobile robot navigation.Artificial Intelligence ,99(1):21–71, 1998.

[11] Vikas Shivashankar, Rajiv Jain, Ugur Kuter, and Dana Na u. Real-time planning for covering an initially-unknown spatial environment.In Twenty-Fourth International FLAIRS Conference , 2011.