利用适应性建议分布和选择性重采样提高基于栅格的Rao-Blackwellized粒子滤波

摘要：

最近，Rao-Blackwellized粒子滤波已被引入作为有效的同时定位和地图创建（SLAM）问题的解决方法。该方法使用粒子滤波器，其中每个粒子携带一个环境的地图。因此，关键问题是如何减少粒子数量。在本文中，我们提出了适应性技术以减少Rao-Blackwellized粒子滤波器中的粒子数量来学习栅格地图。我们提出了一种方法来计算精确的建议分布，不仅考虑机器人的移动，还考虑最近的观察结果。这极大地减少了滤波器预测步骤中的机器人位姿的不确定性。此外，我们提出了一种选择性地执行重采样操作的方法，这显著减少了粒子消耗的问题。

I. 引言

建立地图是移动机器人的基本任务之一。过去，有许多研究人员都专注于这个问题。在文献中，移动机器人制图问题通常被称为同时定位和建图（SLAM）问题 [2,4,5,7,8,12,14,16,18]。它被视为一个复杂的问题，因为机器人在定位时需要一个一致的地图，而在获取地图时，机器人需要对其位置有一个良好的估计。位姿和地图估计之间的相互依赖使得SLAM问题变得困难，需要在高维空间中寻找解决方案。

最近，Murphy，Doucet和他们的同事们 [16,4]引入了Rao-Blackwellized粒子滤波器，作为解决同时定位和建图（SLAM）问题的有效方法。Rao-Blackwellized方法的主要问题在于它们的复杂性，以建立准确地图所需的粒子数量来衡量。因此，减少这个数量是这类算法的主要挑战之一。此外，重采样步骤可能会消除正确的粒子。这个效应也被称为粒子耗尽问题 [19]。

在这项工作中，我们提出了两种方法来极大地提高应用于带网格地图的SLAM的Rao-Blackwellized粒子滤波器的性能：

• 一个考虑机器人传感器精度的提议分布，允许以高精度方式绘制粒子。

• 一种自适应重采样技术，它保持合理的粒子多样性，从而降低粒子耗尽的风险。

提议分布是通过评估扫描注册过程得到的与粒子相关的最可能姿态周围的可能性来计算的。这样，最后一次读数在生成新粒子时就被考虑在内，允许根据比仅使用最后一次里程计读数（如[5]和[8]中所述）得到的模型更为详细（因此更准确）的模型来估计系统的演变。这种精细模型的使用有两个效果。地图更准确，因为在考虑了其对机器人姿态的影响后，当前的激光扫描被并入到与每个粒子相关的地图中。随着时间的积累，估计误差明显降低，需要代表后验的粒子数量也更少。第二种方法，自适应重采样策略允许只在需要时执行重采样步骤，保持合理的粒子多样性。这结果在显著减少粒子耗尽问题上有显著效果。

我们的方法已经通过一系列在大规模室内和室外环境中的系统性实验进行了验证。在所有的实验中，我们的方法生成了高度准确的度量地图。此外，所需的粒子数量比以前的方法要少一个数量级。本文的组织结构如下。在下一节讨论相关工作后，我们将解释如何使用Rao-Blackwellized滤波器来解决SLAM问题。第四部分描述了我们的改进。在真实机器人以及模拟中进行的实验将在第五部分进行讨论。

II. 相关工作

到目前为止提出的建图算法可以根据地图表示和底层估计技术进行大致分类。一种流行的地图表示是占用栅格 [15]。虽然这种基于网格的方法在计算上很昂贵，通常需要大量的内存，但它们能够表示任意特征并提供详细的表示。特征基础的表示，如拓扑图或基于地标的地图，由于其紧凑性而具有吸引力。然而，他们依赖于预定义的特征提取器，这意味着环境的一些结构需要提前知道。

估计算法可以根据其底层基本原理进行大致分类。最流行的方法是扩展卡尔曼滤波器（EKF）、最大似然技术和Rao Blackwellized粒子滤波器。EKF方法的有效性源于它们估计地标图和机器人姿态的完全相关的后验。它们的弱点在于必须对机器人运动模型和传感器噪声做出强假设。此外，假设地标能够被唯一识别。如果这些假设被违反，滤波器可能会发散[6]。

一种流行的最大似然算法通过构建一个表示机器人姿态之间空间约束的关系网络，计算给定传感器读数历史的最可能的地图。Gutmann等人[7]提出了一种有效的方法来构建这样的网络，并在运行增量最大似然算法的同时检测循环闭合。当检测到一个循环闭合时，对关系网络进行全局优化。最近，Hahnel等人[9]提出了一种能够使用关联树跟踪多个地图假设的方法。然而，这个树的必要扩展可能阻止这种方法在实时操作中可行。

在Murphy的一项研究中[16]，将Rao-Blackwellized粒子滤波器（RBPF）介绍为解决SLAM问题的有效手段。在RBPF中，每个粒子代表一个可能的机器人轨迹和地图。这个框架随后被Montemerlo等人[14,13]扩展，用于处理带有地标地图的SLAM问题。为了学习准确的网格地图，Eliazar和Parr[5]以及Hahnel等人[8]已经使用了RBPF。尽管第一项工作描述了一种有效的地图表示，但第二项工作提出了一个改进的运动模型，降低了所需粒子的数量。

本文所描述的工作是对Hahnel等人提出的算法的改进[8]。我们的算法并不是使用固定的提议分布，而是在每个粒子基础上即时计算一个改进的提议分布。这允许在生成粒子时直接使用从传感器获取的大部分信息。提议分布的计算类似于Fast SLAM-2算法[12]的计算，但是，后者依赖于预定义的地标。

我们的方法有两个优点。首先，我们的算法以更有效的方式绘制粒子。其次，高精度的提议分布允许使用有效粒子的数量作为一个稳健的指标，来决定是否需要进行重采样。这进一步减少了粒子耗尽问题。

III. RAO-BLACKWELLIZED建图

Rao-Blackwellized粒子滤波器用于SLAM的关键思想是估计一个关于潜在轨迹$x_{1:t}$的后验$p(x_{1:t}|z_{1:t},u_{0:t})$，这些轨迹是基于其观察值$z_{1:t}$和测距测量值$u_{0:t}$的，然后使用这个后验来计算地图和轨迹的后验：

$$p(x_{1:t}, m|z_{1:t}; u_{0:t}) = p(m|x_{1:t},z_{1:t})p(x_{1:t}|z_{1:t}, u_{0:t})\tag{1}$$

这个计算可以高效地完成，因为如果知道$x_{1:t}$和$z_{1:t}$，就可以以解析方式计算地图的后验$p(m|x_{1:t},z_{1:t})$[15]。

为了估计潜在轨迹的后验$p(x_{1:t}|z_{1:t}, u_{0:t})$，Rao-Blackwellized建图使用了一个粒子滤波器，在该滤波器中，每个样本都与一个独立的地图关联。每张地图都是根据观察值$z_{1:t}$和由相应粒子代表的轨迹$x_{1:t}$构建的。机器人的轨迹按照机器人的运动进行演化，因此选择的提议分布等同于概率性的里程计运动模型。

其中最常见的粒子滤波算法之一是采样重要性重采样（SIR）滤波器。用于建图的Rao-Blackwellized SIR滤波器会在观测和测距读数可用时进行增量处理。这通过更新一组样本来表示关于地图和车辆轨迹的后验概率来实现。具体而言，这可以通过执行以下四个步骤来完成：

1）采样：下一代粒子$\{x^{(i)}_t\}$是从当前代$\{x^{(i)}_{t-1}\}$通过从提议分布$\pi (x_t|z_{1:t},u_{0:t})$中采样而获得的。

2）重要性权重：根据以下公式，给每个粒子分配一个个别重要性权重

$$w^{(i)}=\frac{p(x^{(i)}_t|z_{1:t}, u_{0:t})}{\pi (x^{(i)}_t|z_{1:t}, u_{0:t})}\tag{2}$$

权重 $w^{(i)}$ 考虑到了提议分布 $\pi$ 通常不等于后续状态的真实分布的事实。

3）重采样：通常会用高权重的样本替换具有低重要性权重$w$的粒子。由于只使用有限数量的粒子来近似连续分布，所以这一步是必要的。此外，当真实分布与提议分布不同的情况下，重采样允许应用粒子滤波。

4）地图估计：对于每个位姿样本 $x^{(i)}$，根据轨迹和观察历史，根据 $p(m^{(i)}_t|x^{(i)}_{1:t},z_{1:t})$ 计算出相应的地图估计 $m^{(i)}_t$。

在粒子滤波器的文献中，已经描述了几种计算更好的建议分布和减少粒子耗尽问题的方法[3,17]。我们的方法应用了Doucet[3]描述的两个概念：计算最优提议分布和适应性重采样技术。这两个概念中的第一个已经在基于地标的建图中成功应用于FastSLAM-2 [12]，而据我们所知，适应性重采样从未在使用Rao-Blackwellized粒子滤波器的映射背景中进行过研究。

IV. 改进的提议和自适应重采样的RBPF

虽然通用算法为Rao-Blackwellized建图指定了一个框架，但它没有明确提议分布是如何计算的，以及何时应该进行重采样。在本文的余下部分，我们将描述用于计算准确提议分布的技术，以及自适应确定何时进行重采样。这两种方法都导致了一种高效的Rao-Blackwellized建图技术，该技术需要的粒子数量比以前的基于网格的同类型方法少一个数量级。

A. 计算改进的提议分布

如第三部分所述，在预测步骤中需要从建议分布中抽取样本。这个分布应该近似于真实分布p(xt|z1:t;u0:t)，并且可以任意选择。

根据Doucet [3]，关于粒子权重的方差以及在Markov假设下，提议分布的最优选择是

$$p(x_t|m^{(i)}_{t-1},x^{(i)}_{t-1},z_t,u_t)=\frac{p(z_t|m^{(i)}_{t-1},x_t)p(x_t|x^{(i)}_{t-1},u_t)}{\int p(z_t|m^{(i)}_{t-1},x^\prime)p(x^\prime |x^{(i)}_{t-1},u_t)dx^\prime} \tag{3}$$

在一些粒子滤波应用中[1,14]，里程计运动模型 $p(x_t|x_{t-1},u_t)$ 被选择为提议分布。当建模带激光测距仪的移动机器人时，这种选择可能不是最优的，因为激光测距仪的精度导致似然函数呈极端尖峰。在这种情况下，似然函数 $p(z_t|m^{(i)}_{t-1},x_t)$ 在分布的有意义区域内主导了乘积 $p(z_t|m^{(i)}_{t-1},x_t)p(x_t|x^{(i)}_{t-1},u_t)$ （见图1）。因此，在我们当前的系统中，我们通过一个常数$k$在区间 $L^{(i)}$ 内来近似 $p(x_t|x^{(i)}_{t-1},u_t)$，该区间由以下公式给出：

$$L^{(i)}=\{x|p(z_t|m^{(i)}_{t-1},x)> \epsilon\}\tag{4}$$

在这个近似下，公式 (3) 变为：

$$p(x_t|m^{(i)}_{t-1},x^{(i)}_{t-1},z_t,u_t)\approx \frac{p(z_t|m^{(i)}_{t-1},x_t)}{\int_{x\prime \in L^{(i)}}p(z_t|m^{(i)}_{t-1},x\prime)dx^\prime}\tag{5}$$

此外，我们还通过一个高斯分布来局部近似似然函数的最大值周围的分布：

$$p(x_t|m^{(i)}_{t-1},x^{(i)}_{t-1},z_t,u_t)\approx \mathcal{N}(\mu^{(i)}_t,\mathcal{\sum}^{(i)}_t)\tag{6}$$

通过这个近似，我们得到了一个适合采样的闭合形式。对于每个粒子 $i$，参数 $\mu^{(i)}_t$ 和 $\Sigma^{(i)}_t$ 可以通过对在扫描匹配过程中找到的相应局部最大值周围采样的一组点 ${x_j}$ 评估似然函数来确定。

$$\mu^{(i)}_t = \frac{1}{\eta}\sum^K_{j=1}x_j p(z_t|m^{(i)}_{t-1},x_j)\tag{7}$$ $$\mathbf{\sum}^{(i)}_t = \frac{1}{\eta}\sum^K_{j=1}p(z_t|m^{(i)}_{t-1},x_j)(x_j-\mu^{(i)}_t)(x_j-\mu^{(i)}_t)^T\tag{8}$$

其中，$\eta = \sum^K_{j=1}p(z_t|m^{(i)}_{t-1},x_j)$ 是一个归一化常数。注意，对于每个粒子，$\mu^{(i)}_t$ 和 $\Sigma^{(i)}t$ 的计算以及扫描匹配过程都是针对每个粒子进行的。$\{x_j\}$ 被选择为覆盖根据最后一次里程计读数不确定性 $x_j \in \{x_t|p(x_t|x_{t-1},\mu _t) > \mathcal{X} \}$ 的区域，并且密度取决于网格地图的分辨率。在我们当前的系统中，我们采用了类似于Hahnel等人[10]的扫描匹配例程。

此外，我们需要说明在这个提议分布下如何计算重要性权重。我们可以通过以下方式近似计算第$i$个粒子的重要性权重 $w^{(i)}$：

$$w^{(i)}_t=w^{(i)}_{t-1}p(z_t|m^{(i)}_{t-1},x^{(i)}_{t-1},u_t)\\ =w^{(i)}_{t-1}\int p(z_t|m^{(i)}_{t-1},x^\prime)p(x^\prime|x^{(i)}_{t-1},\mu_t)dx^\prime\\ \simeq w^{(i)}_{t-1} k\int_{x\in L^{(i)}}p(z_t|m^{(i)}_{t-1},x^\prime)dx^\prime\\ \simeq w^{(i)}_{t-1}k\sum^K_{j=1}p(z_t|m^{(i)}_{t-1},x_j) \\ = w^{(i)}_{t-1}k\eta \tag{9}$$

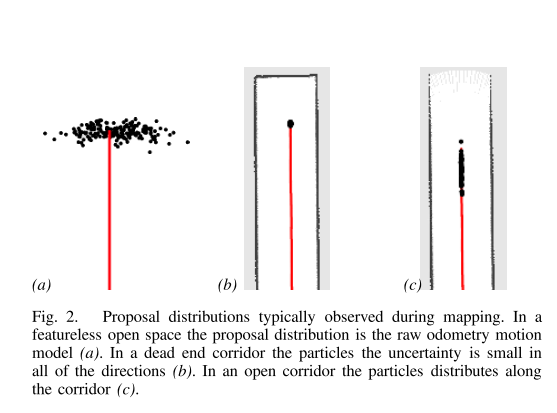
基于我们的似然函数的提议分布使得配备激光测距仪的机器人能够以非常准确的方式进行抽样（见图2）。例如，在走廊中，样本通常沿着其方向分布。由此产生的密度比使用里程计运动模型时的情况具有更低的不确定性。因此，我们的技术允许大大减少粒子数量。与Hahnel等人[8]的方法相比，其使用从扫描匹配过程的残差误差获得的固定提议分布，原则上需要一个保守的提议分布以覆盖最坏情况，因此通常需要更多的粒子。

B. 选择性重采样

对于粒子滤波器的性能影响很大的另一个方面是重采样步骤。在重采样过程中，通常会用具有较高权重的样本替换具有较低权重的粒子。一方面，重采样是必要的，因为只使用了有限数量的粒子。另一方面，重采样步骤可能会从样本集中删除好的样本，导致粒子耗尽[19]。因此，找到何时进行重采样的标准非常重要。

Liu[11]引入了所谓的有效粒子数 $N_{eff}$ 来估计当前粒子集合对真实后验的表示程度。该数量的计算方式如下：

$$N_{eff} = \frac{1}{\sum^N_{i=1}(w^{(i)})^2}\tag{10}$$

$N_{eff}$ 的背后的直觉是：如果样本是从真实后验中抽取的，样本的重要性权重将相互相等。近似程度越差，重要性权重的方差越高。由于 $N_{eff}$ 可以被视为重要性权重的离散度量，它是评估粒子集合对真实后验的逼近程度的有用指标。我们的方法遵循Doucet[3]提出的方法来确定是否应该进行重采样。每当 $N_{eff}$ 降至给定阈值 $N/2$ 以下时，我们进行重采样，其中 $N$ 是粒子的数量。在我们的实验中，我们发现这种方法极大地降低了替换好粒子的风险，因为重采样操作的数量减少了，且只有在需要时才进行重采样操作。

V. 实验

上述方法已在真实的机器人数据上进行了实现和测试。在线实现使用了一台装备有Sick PLS测距仪的Pioneer2 AT机器人。在各种环境中进行的实验表明我们的方法在室内和室外环境中都非常有效。地图的质量非常好，有时候可以生成1cm分辨率的地图，而且几乎没有明显的不一致性。即使在面积为250*250米的环境中，我们也从未使用超过100个粒子。我们的算法可以在Pentium IV-2.8GHz上以50个粒子的实时方式运行，机器人的移动速度为0.5m/s。在下一节中，我们将讨论该滤波器在三个真实世界数据集中的行为。我们的方法生成的更多地图可以在网络上找到。此外，我们对所提出方法的性能进行了定量分析。

A. 地图结果

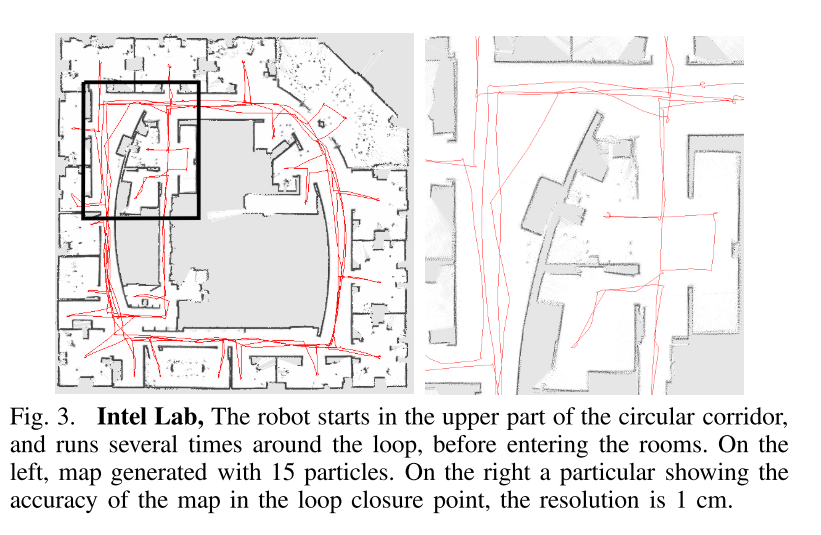
这里讨论的数据集是在西雅图Intel研究实验室、MIT的Killian Court和弗莱堡大学校园录制的。这些环境的地图如图3、4和5所示。

a) Intel实验室：Intel实验室的大小为28*28米。该数据集是使用装备有SICK传感器的Pioneer II机器人录制的。我们的算法只需要15个粒子来处理这个数据集。从图3中可以看出，最终地图的质量非常高，即使将地图放大到1cm的分辨率，也没有明显的可观察到的错误。

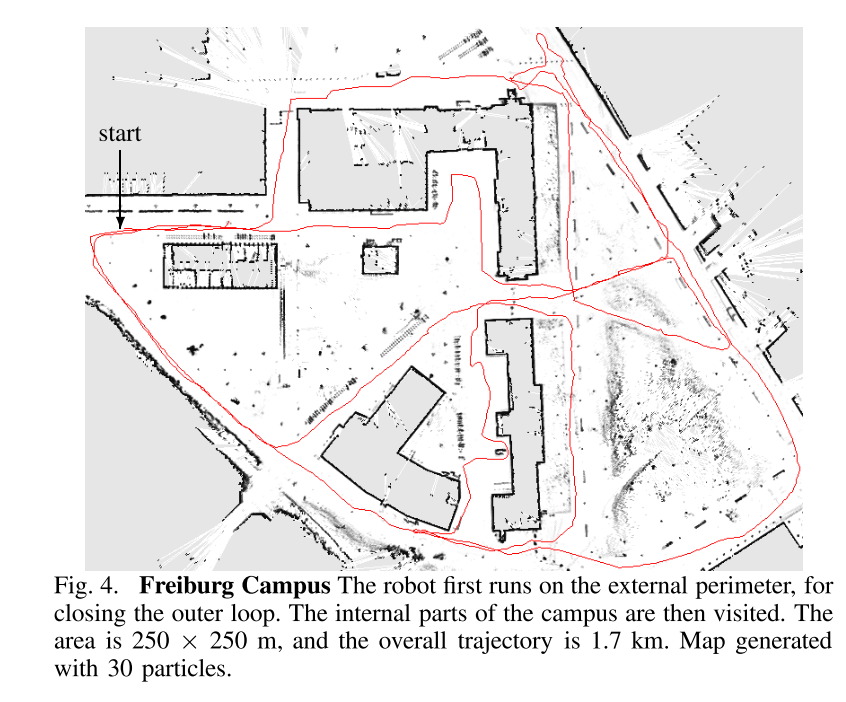
b) 弗莱堡大学校园：第二个数据集是在弗莱堡大学校园的室外录制的。我们的方法只需要30个粒子就能生成一个高质量的地图，如图4所示。请注意，这个环境在某种程度上违反了环境是平面的假设。此外，还有草地、灌木丛以及汽车和人等移动物体。尽管存在一些噪声测量，但我们的算法能够生成准确的地图。

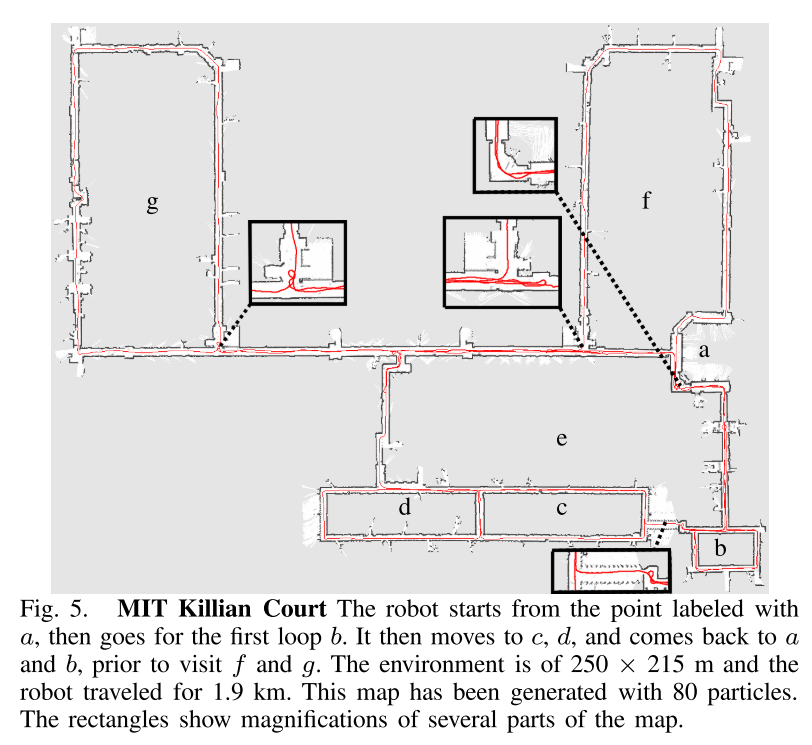
c) MIT Killian Court: 第三个实验是在MIT Killian Court的数据集上进行的（见图5）。对于Rao-Blackwellized mapper来说，这个数据集非常具有挑战性，因为存在几个嵌套的循环，这可能会导致粒子耗尽而使算法失败。在这个数据集中，我们的选择性重采样过程非常有用，因为它保持了关于潜在轨迹的假设。可以使用60个粒子生成一张一致且拓扑正确的地图。然而，生成的地图有时会显示出人工的双重墙壁。通过使用80个粒子，可以获得高质量的地图。

B. 定量结果

为了衡量粒子数量方面的改进，我们比较了我们的知情提议分布和[8]中使用的无信息提议的性能。下表总结了RBPF在我们算法的所有应用中至少提供拓扑正确地图所需的粒子数量。

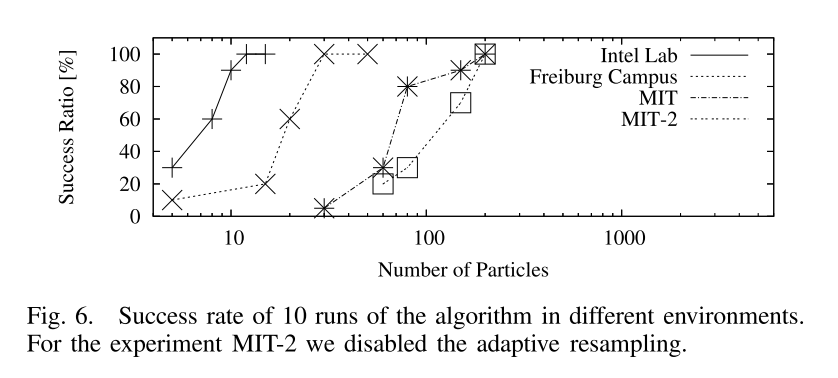
结果显示，在所有情况下，我们的方法所需的粒子数量约为其他方法所需数量的一个数量级。此外，由于我们改进的采样过程考虑了最后一次读数，生成的地图质量更好。图6总结了我们算法在所考虑环境中的成功率结果。图中显示了根据使用的粒子数量的正确生成地图的百分比。地图的质量通过视觉检查进行评估。作为成功的衡量标准，我们使用了拓扑正确性。

C. 改进提议分布和自适应重采样的效果

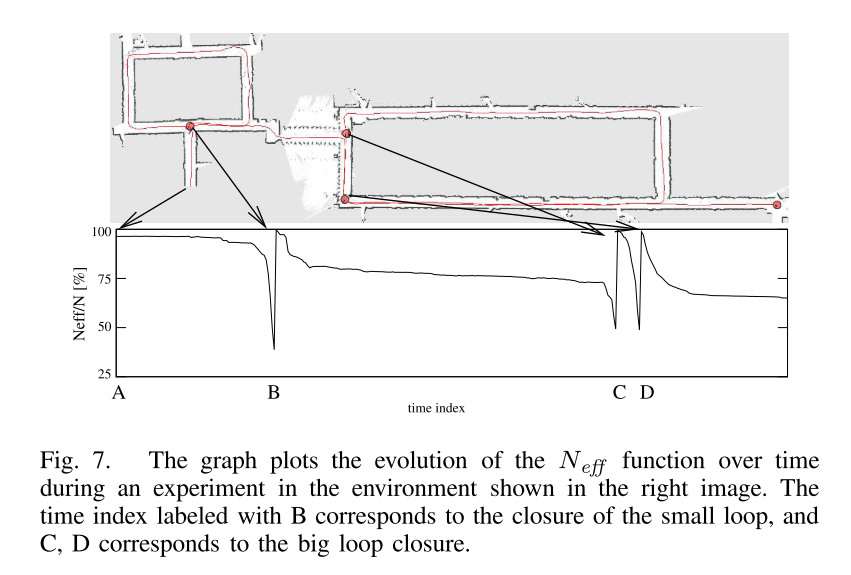
我们方法的性能提升是由两个因素相互作用导致的，即改进的提议分布和通过监测$N_{eff}$控制的自适应重采样。对于不考虑整个输入历史的提议，已经证明$N_{eff}$只能随着时间的推移（随机地）下降[3]。只有在采样操作之后，$N_{eff}$才能恢复到最大值。值得注意的是，$N_{eff}$的行为严格依赖于提议分布：提议越差，$N_{eff}$下降越快。在我们的实验中，我们发现根据机器人传感器获取的信息，我们的提议分布下$N_{eff}$表现出三种不同的行为。当机器人穿越未知地形时，$N_{eff}$通常会缓慢下降。这是因为提议分布变得不那么尖峰，观测的可能性通常略有不同。第二种行为可以观察到当机器人穿越已知区域时。在这种情况下，由于改进的提议分布，每个粒子都保持在自己的地图中，权重或多或少相等，这取决于所获取的扫描和地图之间的不一致性的程度。这导致$N_{eff}$保持稳定。最后，在闭环时，一些粒子与它们的地图正确对齐，而其他一些粒子则没有。正确的粒子具有较高的权重，而错误的粒子具有较低的权重。因此，重要性权重的方差增加，$N_{eff}$显著下降。因此，我们对$N_{eff}$的阈值准则通常会在机器人闭环时进行重采样。在其他所有情况下，会避免重采样，以保持粒子集中的必要多样性。结果，粒子耗尽问题得到了严重缓解。为了分析这一点，我们进行了一个实验，将我们的算法的成功率与每步都进行重采样的粒子滤波器进行了比较。如图6所示，与具有相同数量粒子和固定重采样策略的粒子滤波器（MIT -2曲线）相比，我们的方法更常收敛于正确解（MIT曲线）的MIT数据集。

参考文献

[1]F.Dellaert, D.Fox,W.Burgard, andS.Thrun.Monte carlo localization formobile robots.In Proc.of the IEEE Int.Conf .on Robotics & Automation (ICRA) ,1998.

[2]G.Dissanayak e,H.Durrant-Whyte, and T.Baile y.A computationally efficient solution to the simultaneous localisation and map building (SLAM) problem.In ICRA ‘2000 Workshop onMobile Robot Navigation andMapping ,2000.

[3]ADoucet.On sequential simulation-based methods for bayesian filtering. Technical report, Signal Processing Group, Departement of Engeneering, University ofCambridge, 1998.

[4]A.Doucet, J.F.G.deFreitas, K.Murphy ,and S.Russel.Rao-blackwellized partcile filtering for dynamic bayesian netw orks.In Proc.of the Conf .on Uncertainty in Artificial Intelligence (UAI),2000.

[5]A.Eliazar and R.Parr.DP-SLAM: Fast,robust simultainous localization and mapping without predetermined landmarks.In Proc.of the Int.Conf .on Artificial Intellig ence (IJCAI) ,2003.

[6]U.Frese andG.Hirzinger .Simultaneous localization and mapping -adiscussion.In Proc.of the Int. Conf .on Artificial Intelligence (IJCAI) ,2001.

[7]J.-S. Gutmann and K.Konolige.Incremental mapping of large cyclic environments.In Proc. of the International Symposium on Computational Intelligence in Robotics and Automation (CIRA) ,2000.

[8]D.H¨ahnel, W.Burgard, D.Fox,and S.Thrun. An efficient FastSLAM algorithm for generating maps of large-scale cyclic environments from raw laser range measurements.
In Proc. of the IEEE/RSJ Int.Conf .on Intelligent Robots and Systems (IROS),2003.

[9]D.H¨ahnel, W.Burgard, B.Wegbreit, and S.Thrun. Towards lazy data association in slam.In Proc. of the International Symposium of Robotics Resear ch(ISRR) ,2003.

[10] D.H¨ahnel, D.Schulz, and W.Burgard. Map building with mobile robots inpopulated environments.In Proc. of the IEEE/RSJ Int. Conf .on Intelligent Robots and Systems (IROS),2002.

[11] J.S.Liu.Metropolized independent sampling with comparisons to rejection sampling andimportance sampling. Statist. Comput.,6:113-119, 1996.

[12] M.Montemerlo, S.Thrun D.Koller,andB.Wegbreit.FastSLAM 2.0:An improved particle filtering algorithm for simultaneous localization and mapping that provably converges.In Proc.of the Int. Conf .on Artificial Intelligence (IJCAI) ,2003.

[13] M.Montemerlo andS.Thrun. Simultaneous localization and mapping with unknown data association using FastSLAM. In Proc. of the IEEE Int. Conf . on Robotics &Automation (ICRA) ,2003.

[14] M.Montemerlo, S.Thrun, D.Koller,and B.Wegbreit.FastSLAM: A factored solution to simultaneous localization and mapping. In Proc. of the National Conference on Artificial Intelligence (AAAI) ,2002.

[15] H.P.Mora vec.Sensor fusion incertainty grids for mobile robots.AI Magazine ,pages 61–74, Summer 1988.

[16] K.Murphy .Bayesian map learning indynamic environments.In Neural Info. Proc. Systems (NIPS) ,1999.

[17] M.K. PittandN.Shephard.Filtering via simulation: auxilary particle filters.Technical report, Department of Mathematics, Imperial College,London, 1997.

[18] S.Thrun.An online mapping algorithm for teams of mobile robots. International Journal of Robotics Research,2001.

[19] R.vanderMerwe, N.deFreitas, A.Doucet, and E.Wan.Theunscented particle filter.Technical Report CUED/F-INFENG/TR380,Cambridge University Engineering Department, August 2000.