采用快速无碰撞路径生成器的安全的基于深度学习的全局路径规划

Chehelgami S, Ashtari E, Basiri M A, et al. Safe deep learning-based global path planning using a fast collision-free path generator[J]. Robotics and Autonomous Systems, 2023, 163: 104384.

摘要

在本研究中，我们提出了一种基于循环神经网络的全局路径规划方法，通过新的损失函数来实现。该方法无论配置空间的复杂性如何，都能在相对恒定的时间内生成路径。新的损失函数被定义为除了学习网络的输入数据外，还在障碍物周围创建一个可调的安全边距，从而最终生成一个安全的路径。

此外，我们还引入了一种新的全局路径规划方法，用于创建训练所提议的神经网络所需的数据集。这种方法的收敛性已得到数学证明，并且已经表明，与文献中报道的常见的全局路径规划方法相比，该方法可以在更短的时间内生成一个次优路径。

简而言之，本研究的主要目的是提供一种方法，该方法能够为移动机器人在已知环境中从任意随机起点到任意随机目的地创建一个次优、快速且安全的路径。

首先，提议的方法将被应用于由凸形和非凸形障碍物组成的不同二维环境中，并将机器人视为一个质点，然后它将在3D仿真环境AI2THOR中实施。与传统的全局路径规划算法（如RRT和A*）相比，所提议的方法在复杂且具有挑战性的环境中表现更好。

1. 引言

移动机器人最重要的特性之一是路径规划，它减少了它们对人工干预的依赖 [1]。在机器人技术中，路径规划涉及到确定目的地并找到一系列动作，使机器人能够从其当前状态安全地到达预定的目标点，而不会遇到环境中的障碍物 [2]。存在多种从起点到终点生成无碰撞路径的方法，当机器人周围的环境从一开始就已知时，这些方法中最常见的是基于网格的方法和基于采样的方法。

在基于网格的方法中，如A [3]，配置空间维度上的网格数量呈指数增长，使它们不适合于高维环境 [4]。然而，A 算法已经在多个领域得到应用，例如自动化、机器人技术 [5]、医学 [6] 和游戏 [7]。像RRT [8] 这样的基于采样的方法并不高度依赖于环境的维度，但随着环境的复杂性增加，它们的执行速度急剧下降，对于在具有复杂约束的环境中进行精确的运动规划，它们在计算上是不可行的 [9]。然而，RRT算法已经在各种领域得到应用，如自动化、机器人技术 [10]、移动机器人的路径规划 [11] 等。

由于理想的路径规划算法应解决真实世界问题，提供诸如路径的完整性和最优性、对维度和环境复杂性的不敏感性、计算效率等关键特性，现有算法之间存在基本的权衡关系，并且已有少数运动规划器被提议来解决后述问题 [12]。

很多研究已经使用深度神经网络来解决路径规划的问题 [13] [14] [15]，由于计算机硬件和人工智能算法的同步进步，近年来在这个领域取得了大量的进展。从文献中提出的研究可以看出，使用深度神经网络进行路径规划对于创建准确、快速和最优的运动规划器具有巨大的潜力 [12]。

在 [16] 中，提出了一种有趣的方法，称为OracleNet，它基于深度神经网络，为静态环境产生快速和最优的无碰撞路径。在这项研究中，使用LSTM网络通过减少损失函数来创建次优路径。这个简单的算法几乎在恒定的时间内创建这些次优路径，因此，这种方法比在复杂环境和更高维度中的路径规划算法更受欢迎，其中他们的计算量增加，从而路径的生成速度减慢。

在这篇论文中，训练数据集包括由RRT和A*路径规划器创建的一些路径，如前所述，随着状态空间的大小或复杂性的增加，这些算法的速度会降低，使用这些方法生成训练数据将是耗时的。此外，用于训练这个网络的损失函数是MSE，它对障碍物及其位置没有任何感觉，这会导致预测路径出错，而在很多情况下，预测的路径会穿过障碍物的角落，因此，网络将无法预测无碰撞路径。因此，尽管所提议的模型导致了可接受的性能，并在短时间内产生了次优路径，但它包含一些缺点，解决它们后将导致一个安全和自信的路径规划方法。

在本文中，作为第一步，我们提出了一种基于Bug2局部路径规划算法的快速和高效的全局路径规划方法，称为Fast Global Bug (FGB)。据作者所知，FGB方法比其他现有的全局路径规划方法更快，且不太依赖于环境的复杂性和维度。已经证明，由于其高速性，所提出的算法可以用于创建神经网络训练所需的数据。然后，为移动机器人路径规划提出了一个新的损失函数。所呈现的损失函数，除了学习训练数据外，还有一个排斥项，该排斥项将路径的预测点从其最近的障碍物的最近点移开，从而在障碍物周围创建一个安全可调的边距。这将增加路径规划的成功率，尤其是在复杂的环境中。

所提出的方法在不同环境中的点机器人和AI2THOR [17] 平台上的虚拟机器人的结果都得到了展示。鉴于在任何新环境中，所提议的网络都需要训练，该算法适用于在静态环境中工作的机器人（如仓库、购物中心、机场航站楼等）。然而，通过将这种方法与局部路径规划算法，人工势场 (APF) [18]，结合起来，也在 [19] 中提出了一个可以用于动态环境的混合路径规划算法。

本文的其余部分组织如下。第2节提供了文献中对移动机器人路径规划进行的研究的概述。第3节提供了所提议的模型的详细信息以及用于比较的替代方法。第4节和第5节给出了实验结果，最后一节总结了所有内容。

2. 相关工作

在本文中，为了提出一种新的路径规划方法，该项目的不同部分使用了几种先前的路径规划方法。因此，在这一部分，在提出新的路径规划方法之前，我们将回顾一些如A* [3]、RRT [8]、势场 [18]、BUG [20] [21] 和 Oracle Net [16] 等路径规划方法。

2.1. A*

这种方法是一种图搜索方法，其中环境被划分为离散点或节点，并且可以只考虑这些节点来获得到目标的最短路径。选择适当节点的方法之一是$A^*$方法。在此方法中，节点以规律的方式被添加到图中，并且通过优先考虑更有可能产生最优路径的节点来进行此操作 [22]。为此，除了节点的成本外，还使用了一些探索方法，例如从一个节点到目标的直线距离，两个函数的总和表示路径的成本：

$$f(n) =g(n) +h(n) \tag{1}$$

如上所述，上述成本函数有两个参数：$g(n)$：从主单元到当前单元的转移成本，本质上是从第一个单元访问的所有单元的总和。$h(n)$：也被称为探索值，是从当前单元移动到最终单元的估计成本。在达到最终单元之前，无法计算实际成本。因此，$h(n)$ 是估计成本 [23]。然而，在如$A^*$这样的算法中，在连接的图表或网络中进行搜索，在小型和简单的环境中是快速和优化的，但随着环境的大小和其复杂性的增加，它们的计算会扩展，这导致了路径的产生速度减慢 [24]。

2.2.快速探索随机树 (RRT)

所谓的RRT（Rapidly-exploring Random Tree）路径规划方法是由Lavalle和Kuffner [8] 开发的，用于在配置空间中找到路线。在RRT方法中，过程从第一个节点开始，将向树中添加一个新节点，但距离不能太远，因为在这种情况下，通过障碍或过多地朝错误方向移动的概率增加；因此，指定了一个最大距离，使新节点可以靠近最后一个节点。在这种情况下，会发生几种情况；如果随机节点比最大距离更近，则新节点将被放在那里。如果节点之间存在障碍，并且新节点应该放在那里，那么新节点将被忽略，不会被添加到树中，并继续添加新节点，这防止树通过障碍 [25]。所以，在每个阶段，选择一个新节点，然后找到离它最近的节点。随着新节点数量的增加，路径进入未知区域，因此环境被快速探索，这就是这个算法被称为Rapidly-exploring Random Tree的原因。这个过程继续，直到路径距目标一定距离。尽管此方法产生的路径是之字形的且未经优化，但生成的路径使用的节点比A*少，因为节点之间可以有更大的距离。RRT在只需求一个有效路径以及开始和目标节点可用的情况下工作得很好 [11]。

2.3.人工势场

人工势场方法（APF）最初由Khatib于1986年提出，用于移动机器人的路径规划[18]。在APF方法中，机器人被视为机器人配置空间中的一个质点，并受到像粒子一样的人工势场的影响。APF算法使用人工势场来调整机器人在特定空间中的移动。在这种方法中，远离目标的区域具有高势能，而当机器人接近目标时，势能逐渐减少，直到在目标点时，势能变为零。这种方法的主要思想是想象所有障碍物都可以为机器人产生排斥力，而目标点为机器人产生吸引力。机器人施加与吸引和排斥力的梯度相关的力。因此，机器人的运动方向矢量可以通过结合吸引和排斥力来描述。指定机器人移动的最终力量如下[26]：

$$F=F_{att}+F_{rep} \tag{2}$$

在[26]中，APF方法用于在目标和障碍物都在移动的动态环境中的移动机器人的运动规划。机器人的速度和路径由障碍物和目标的相对速度和方向决定。仿真结果证实，这种方法可以有效地追踪移动的目标，同时避免其路径上的障碍。

APF方法为机器人路径规划提供了一个简单而有效的方式，但它也有缺点。这种方法的主要问题是，在达到目标之前，机器人经常陷入局部最小值。当所有人工力（吸引和排斥）相互抵消时，就会出现这个问题，例如当障碍物恰好在机器人和目标之间，或者当障碍物彼此靠近时。为了克服这个问题，已经提出了几种方法[27]。例如，解决这个问题的一个简单方法是在机器人的运动中加入随机噪声，这可以使机器人避免局部最小值。

2.4.爬行虫算法

Bug算法非常适合在资源有限的情况下进行室内机器人路径规划，因为这些算法只需要很少的内存和处理能力，所以它们预计会在内部计算机中占用很小的空间[28]。该算法的基本原理是，机器人不知道其环境中障碍物的位置，只知道其目的地的相对位置。换句话说，机器人只在与障碍物和墙壁接触时做出反应，允许机器人通过沿着障碍物的边界移动来朝向其目标（墙壁追踪）[29]。Lumelsky和Stepanov[20]是这项技术的开发先驱。最初，他们介绍了一个非常简单的Bug算法，称为“常识算法”，也被称为COM。在这种方法中，机器人只要有可能就朝向目标移动。Bug算法首次撞到障碍物的地方称为撞击点，路径离开障碍物到达目标点的地方称为离开点。似乎COM可以在许多情况下解决路径规划问题。但是，Lumelsky和Stepanov[20]指出，有些情况下机器人无法到达目标点。此外，他们介绍了Bug1算法，并采用了不同的策略来克服COM所面临的问题。在这种策略中，每当路径遇到障碍物时，它首先通过跟随其整个边界来探索障碍物，同时找到边界上距离目标点最近的位置并存储在内存中。与第一个撞击点发生碰撞后，路径将朝向离目标最近的位置并离开障碍物。本文还显示，路径的长度永远不超过以下限制：

$$P = d(S;T) + 1.5\times \sum p_i \tag{3}$$

其中$P$是整个路径的长度，$d(S;T)$是起点和目标点之间的距离，而$p_i$是第$i$个障碍物的边界长度。

然而，这个算法是一种不太直观的方法，因为它需要探索障碍物的整个边界，所以会产生不必要的长路径。因此，一年后，Lumelsky和Stepanov [21] 发现了Bug1算法在路径长度上的非最优性，因此提出了Bug2作为另一种替代方法。在这个算法中，从起点到目标点之间考虑了一条假设线，称为m线，然后路径会探索障碍物的边界，直到在另一侧击中$m$线；如果这个点比初始击中点更接近目标点，路径将从那个点离开障碍物。在[21]中，证明了后一种方法将路径的最大长度减少到：

$$P = d(S;T) + \sum p_i \tag{4}$$

2.5. Oracle Net

在[16]中，引入了一种名为OracleNet的新方法，它使用基于神经网络的路径生成器，能够在静态环境中以固定时间产生所需的路径。此外，使用了一种叫做长短时记忆（LSTM）[30]模型作为循环神经网络（RNN）。为了生成训练数据集，使用了一些路径规划器，如RRT和A*，并且文章使用均方误差[31]作为损失函数。该网络通过减小损失函数来学习训练数据集中的路径，最终为环境中的每个随机起点和目标点预测出相对平滑的路径。在实践中，OracleNet能够在固定的短时间内生成路径，而不受配置空间复杂性的影响，并且在复杂环境和更高维度中表现比常见的路径规划算法更好。

3. 训练数据生成

本文介绍了一种新的数据创建方法，该方法受到了对Bug2算法进行一些修改的启发。Bug2算法使用机器人的传感器和环境的局部知识来在实际环境中进行路径规划和避障。但是这种新方法，称为快速全局Bug（FGB），是为了在静态环境中获取路径作为训练数据。在这种方法中，假设有关环境的全局知识，包括障碍物的角点坐标、起点和目标点的坐标是已知的。

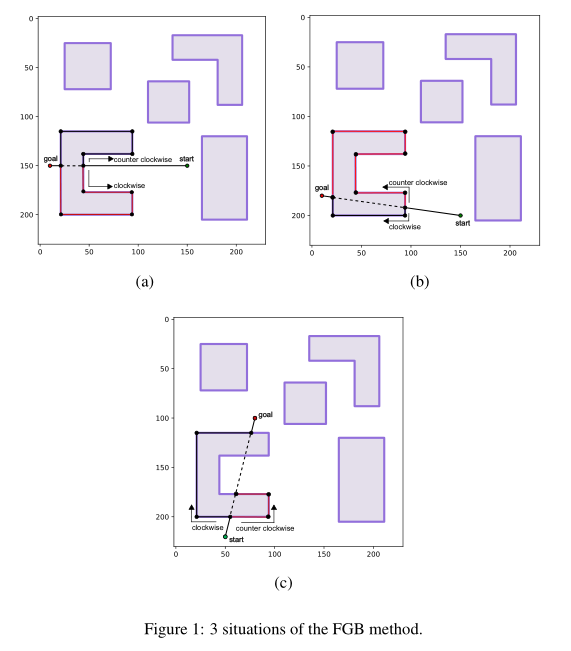
在FGB方法中，从起点到目标点之间考虑了一条直线，即上文提到的$m$线，并确定了与障碍物发生碰撞的点，称为击中点。通过将从起点到目标的击中点排列好，路径从起点开始沿着$m$线前进，直到到达第一个击中点。到达击中点后，路径被虚拟地分成两个分支，顺时针和逆时针，并在障碍物周围的两个方向上继续前进，记录下已经通过路径的障碍物的角点，这导致了两种常见情况：

1. 两个路径中的一个达到下一个击中点，通过较少的障碍物角点，选择该路径。
2. 两个路径都通过相同数量的障碍物角点达到下一个击中点，在这种情况下，有两种情况发生：
   (a) 两个路径都达到一个击中点，计算从两个方向到这个击中点的距离，选择距离较短的路径。
   (b) 两个路径到达不同的击中点，选择距离目标更近的击中点的路径。
   然后，路径继续沿着$m$线，重复相同的过程，直到路径结束在目标点。图1以示例的方式概述了FGB方法中上述的3种情况，并且需要提到本文中的图形单位是分米。到达目标后，已获得了一条从起点到目标的无碰撞路径，但因为它沿着直线从起点到目标并绕过障碍物，所以它不是最优路径，具有一些多余的点，使路径变长。

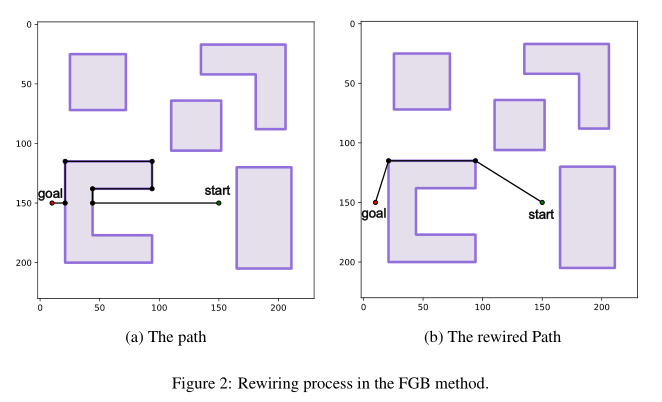
为了解决这个问题，采用了在[16]中介绍的一种重连过程；在这个过程中，如图2所示，如果连接路径中两个非连续节点的直线是无碰撞的，那么路径中的不必要节点将被删除。
创建训练数据的算法如算法1所示。

3.1. 收敛性证明

收敛性证明取决于障碍物的类型，即凸障碍和非凸障碍。为了实现对FGB方法生成的路径收敛性的证明，接下来将研究两种类型障碍物的证明。

3.1.1. 针对非凸障碍物

• 定理 3.1.
  FGB方法生成的路径长度始终低于一个限制值。
• 引理 3.2.
  $m$线与非凸障碍物有$n$击中点，其中$n > 2$，$n$为偶数$（n = 2k）$。
• 引理 3.3.
  如果击中点的集合被编号，奇数编号的击中点是m线撞击障碍物的点；换句话说，$m$线在这些自由空间的点上进入了障碍物，而偶数编号的击中点是$m$线离开障碍物并继续在自由空间中的点。
• 引理 3.4.
  根据FGB方法的过程，在障碍物的周边，路径总是从一个离开点到下一个击中点，或从一个击中点到下一个离开点。
• 引理 3.5.
  根据所提出的方法的过程，由于不选择以前的击中点，路径不会陷入局部循环，因此在障碍物的周边的最坏情况是连续通过所有击中点。
  证明。
  根据引理3.5，在最坏的情况下，假设路径通过所有的击中点和离开点。
  路径分为两个方向，左边和右边，然后： $$p^i_{L_j} + p^i_{R_j} ≤ P^i（5）$$ 其中$p$表示周长，$i$表示第$i$个障碍物，$L$和$R$用于确定路径方向，$j$表示第$i$个障碍物的击中次数。

显然，$p^i_{L_j}$和$p^i_{R_j}$是正数，并且小于$p^i$，因为它们实际上是第$i$个障碍物的周长的一部分。
在FGB方法的过程中，根据伪代码需要选择$p^i_{L_j}$和$p^i_{R_j}$的一个方向，然后调用选定的路径$p^i_{j_{selected}}$。因此，选定的$p^i_{j_{selected}}$的值小于$p^i\cdot d_{tot_non-convex}$，由FGB方法在有非凸障碍物存在的情况下生成的路径的最大长度如下所示：

$$d_{tot_non-convex}=d_s+\sum^O_{i=1}((\sum^{n_i}_{j=1,j=2k+1}P^i_{j_{selected}}+\sum^{n_i}_{j=2,j=2k}d_{i_j})+d_{i,i+1})+d_g\tag{6}$$

根据定义，$d_{i_j}$是 $m$ 线的一部分，在自由空间中，位于第$i$个障碍物的第$j$个击中点和第$(j+1)$个击中点之间；$d_{i,i+1}$是$m$线的一部分，在自由空间中，位于第$i$个障碍物的最后一个击中点和第$(i+1)$个障碍物的第一个击中点之间；最后，$d_s$和 $d_g$ 分别是$m$线在自由空间中的第一个段和最后一个段。因此，根据这个定义，显然有：

$$d_s+\sum^O_{i=1}[(\sum^{n_i}_{j=2k,j=2}d_{i_j})+d_{i,i+1}]+d_g\leq D\tag{7}$$

在上述文本中，$D$ 是所有位于自由空间中的$m$线段的总和；同时也有

$$\sum^O_{i=1} \sum^{n_i}_{j=1,j=2k+1} P^i_{j_{selected}} \leq \sum^O_{i=1}\frac{n_i}{2}P^i\tag{8}$$

因此，

$$P_{tot_non-convex}\leq D+\sum^O_{i=1}\frac{n_i}{2}P^i\tag{9}$$

由于 $P^i$ 和$D$都是有限的，而$n^i$也是有限的，因此$P_{tot_non-convex}$也是有限的。因此，由FGB方法生成的路径在非凸形障碍物情况下有一个上限。