使用粒子群优化算法进行机器人在动态环境中的路径规划

A. Z. Nasrollahy and H. H. S. Javadi, “Using Particle Swarm Optimization for Robot Path Planning in Dynamic Environments with Moving Obstacles and Target,” 2009 Third UKSim European Symposium on Computer Modeling and Simulation, Athens, Greece, 2009, pp. 60-65, doi: 10.1109/EMS.2009.67.

摘要

在已知和动态环境中进行机器人路径规划对于移动机器人是可行的，其主要目的是在包含障碍物的环境中找到机器人从初始位置到目标位置的无碰撞路径。在本文中，假设目标位置随时间变化。此外，我们的环境包括移动障碍物和静态障碍物。我们提出了一种新的移动机器人路径规划方法，使用粒子群优化算法，以最小化总路径规划时间，同时避免局部最优解。我们使用模拟来验证和说明这一方法。

1、引言

机器人路径规划的主要问题是根据一些优化标准找到从起始位置到目标位置的运动轨迹。迄今为止，已经付出了大量的努力来解决路径规划的基本问题。一个完美和精确的路径规划器，可以找到路径（如果存在的话），否则会报告没有路径存在，这是NP难问题[6]。路径规划问题的经典技术包括Roadmap、Cell Decomposition、Potential Fields和数学规划等通用方法。大多数路径规划问题都可以使用这些经典技术来解决。然而，在大问题空间中实时响应方面，它们计算上太复杂。为了提高经典方法的效率，提出了像PRM和RRT这样的概率算法。对于局部最优问题，路径规划问题中使用了许多启发式和元启发式算法，如模拟退火、遗传算法和蚁群优化[7, 8, 9]。[10]中提出了一种基于PSO的移动机器人路径规划算法，包括变异运算符。2005年，[2]中讨论了在动态环境中使用多目标PSO进行碰撞预防的方法。[11]中研究了足球机器人的障碍物避免路径规划。最后，在[12]中模拟了移动机器人的平滑路径规划。

在本文中，我们利用PSO来解决机器人路径规划问题，以充分发挥其在动态环境和大规模领域中的能力。通过将PSO作为一种多智能体搜索技术使用，我们希望提出一种高效的搜索算法，同时创建一个小规模的搜索系统模型，以便在障碍物和目标位置的重新定位时规划路径。文章的其余部分组织如下。在第二节中，我们简要介绍粒子群优化算法。第三节讨论了PSO和机器人路径规划问题。我们在第四节中介绍了我们提出的方法。在第五节中，我们讨论如何使用PSO解决约束路径规划问题。第六节致力于实验结果，最后在第七节中进行总结。

2、粒子群优化

PSO是一种用于解决问题的新技术，其解可以表示为$D$维解空间中的一个点。PSO初始化时使用一群随机粒子$（X_1，X_2，\cdots，X_D）$，它们在搜索空间中均匀分布。假设第$i$个粒子的位置和速度分别由$D$维向量$X_i=(x_{i1}, x_{i2},\cdots, x_{iD})$和$V_i=(v_{i1}, v_{i2}, \cdots, v_{iD})$表示。第$i$个粒子的最佳之前位置$(pbest)$定义为$P_i=(p_{i1}, p_{i2}, \cdots, p_{iD})$，而整个种群的最佳位置$（gbest）$由$P_g=(p_{g1}, p_{g2},\cdots, p_{gD})$表示。根据以下方程式更新新的速度和位置：

$$V^{k+1}_i=wV^k_i+c_1r_1(P_i-X^k_i)+c_2r_2(P_g-X^k_i)\tag{1}$$ $$X^{k+1}_i=X^k_i+V^{k+1}_i\tag{2}$$

其中，$i=1, 2,\cdots, N$，$N$是种群的大小；$k=1, 2, \cdots , K$，$K$是最大迭代次数；$w$是惯性权重；$c_1$和$c_2$是两个正常数，通常我们选择$c_1=c_2=2$；$r_1$和$r_2$是在0到1范围内的两个随机函数。在PSO中，速度和位置的约束条件为：

$$-v_{max}\leq v_{id}\leq v_{max},x_{min}\leq x_{id}\leq x_{max} \tag{3}$$

其中，$v_{max}$是最大速度，实际上它充当了一种约束，用来控制PSO的全局探索能力的最大值；$x_{min}$和$x_{max}$是解空间的下限和上限。每个粒子的性能根据一个预定义的适应度函数来衡量，这个函数依赖于具体问题。
每个粒子观察自身和邻居的”适应度”，并通过朝向成功的邻居移动来模拟它们。这种极其简单的方法在各种问题领域都表现出了出乎意料的有效性。

在PSO中，惯性权重$w$扮演着一个非常重要的角色，因为全局和局部探索能力之间的平衡主要由惯性权重控制。因此，参数$w$将影响PSO的收敛行为，选择一个合适的$w$将有助于算法准确而迅速地找到最优解。在搜索开始时，较大的惯性权重有助于找到好的初始种子，而后期较小的惯性权重有助于进行精细搜索。因此，我们开发了一种线性递减的惯性权重技术，从搜索开始时线性变化从0.95到结束时的0.4。这种技术已被证明非常有效，可以在全局和局部探索能力之间取得平衡。因此，我们在研究中使用了这种技术，惯性权重由以下方程确定：

$$w=w_{start}-\frac{w_{start}-w_{end}}{K}k\tag{4}$$

其中，$w_{start}$和$w_{end}$分别表示惯性权重的起始值和结束值。

标准PSO的步骤可以总结如下（算法1）：

• 步骤1：初始化种群大小N
  初始化解空间的维度D
  初始化最大迭代次数K
  初始化惯性权重$w_{start}$和$w_{end}$
• 步骤2：对于每个粒子
  随机初始化粒子位置$X_i$
  随机初始化粒子速度$V_i$
  将当前位置初始化为$P_i$
  评估适应度值
  根据适应度值初始化$P_g$
• 步骤3：根据（4）计算新的惯性权重。
• 步骤4：根据（1）更新每个粒子的速度，
  如果$v_{id} > v_{max}$，则$v_{id} = v_{max}$
  如果$v_{id} < -v_{max}$，则$v_{id} = -v_{max}$
• 步骤5：根据（2）更新每个粒子的位置，
  如果$x_{id} > x_{max}$，则$x_{id} = x_{max}$
  如果$x_{id} < x_{min}$，则$x_{id} = x_{min}$
• 步骤6：评估所有粒子的适应度值。对于每个粒子，将其当前适应度值与其$pbest$的适应度值进行比较。如果当前值更好，则更新$pbest$和其适应度值。此外，确定具有最佳适应度值的当前种群中的最佳粒子。如果适应度值比$gbest$的适应度值更好，则使用当前最佳粒子的位置和目标值更新$gbest$和其适应度值。
• 步骤7：如果达到最大迭代次数或任何其他预定义的标准，则停止；否则返回到步骤3。

3、PSO与机器人路径规划问题

问题表述

机器人路径规划的问题表述是根据其当前位置在一个动态而已知的环境中确定机器人的下一个位置。在考虑一些预定义原则的前提下，这里我们给出了路径规划问题的一个通用和一般性定义：

A. 预设条件

1) 机器人的当前位置已知，相对于给定的参考坐标系。
2) 机器人有一个有限的最大步幅，$V_{robot}$，机器人在每一步中不能走得更远。
3) 目标也有一个最大步幅，$V_{goal}$，它应该小于机器人的最大步幅。否则，尽管目标从来不会移动，每一步都根据概率$P_{goal}$而移动，在最坏的情况下它可以一直逃离机器人。
4) 环境中的每个障碍物都有一个重新定位概率$P_{obs}$。根据这个概率，在每一步开始之前，规划过程开始之前，所有的障碍物都会改变其位置，移动距离为$V_{obs}$。对于静态和不可移动的障碍物，$P_{obs}=0$。
5) 假设障碍物是圆形的。环境中没有两个障碍物重叠。但它们可以相邻。
6) 路径规划算法运行直到机器人距离目标达到预定义的距离（阈值）。

B. 原则

在满足给定的预设条件的前提下，本文中使用了以下原则：

1) 机器人始终选择通往目标的最短路径。
2) 如果机器人到目标的直接路径会与静态和移动障碍物发生碰撞，机器人会在半径为$V_{robot}$的范围内调查其环境，以找到具有最小碰撞的路径的下一个位置。
3) 机器人会旋转以减少与障碍物可能的碰撞。这个旋转可以是运动半径的任意角度，$0\leq \alpha < 2\pi$。

假设$(x_r, y_r)$是机器人在时刻$t$的当前位置，$(x^{\prime}_r, y^{\prime}_r)$是机器人在时刻$(t+1)$的下一个位置，$(x_g, y_g)$是机器人的目标位置。

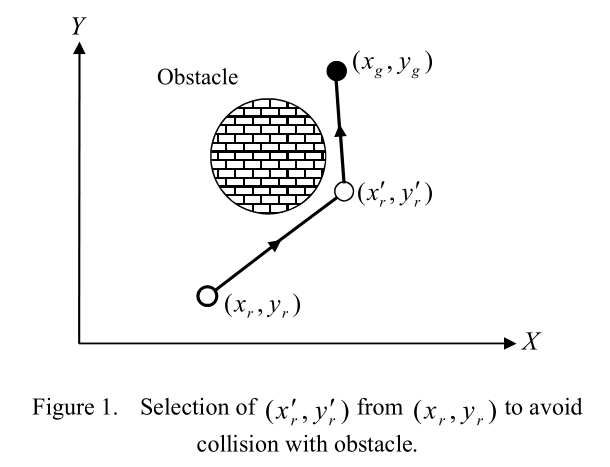
为了找到中间位置$(x^{\prime}_r, y^{\prime}_r)$，我们需要适当地构建PSO算法。因此，我们在这里给出将粒子映射到问题的某个元素的方法。粒子的位置作为机器人路径规划问题的解表示了2维解空间中的一个点。PSO初始化时使用一群随机粒子，它们在初始时在$(x_r, y_r)$周围均匀分布，具有随机的位置和速度。粒子的速度向量的计算方式与其位置相同，根据(6)和(7)计算，但$x_r$和$y_r$设置为0，旋转角度为$\alpha_i$（参见图2）。在算法执行结束时，我们选择具有最佳位置的粒子作为机器人的下一个位置。

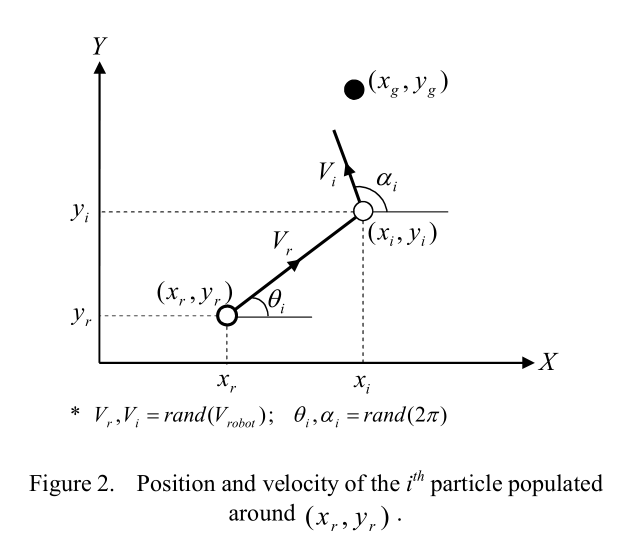
目标函数

假设机器人位于$(x_r, y_r)$。我们需要选择点$(x^{\prime}_r, y^{\prime}_r)$，即机器人的下一个位置，使得连接$\{(x_r, y_r)(x^{\prime}_r, y^{\prime}_r)\}$和$\{(x^{\prime}_r, y^{\prime}_r)(x_g, y_g)\}$的直线不会触碰到图1中的障碍物。实际上，这是通过PSO算法来实现的。由于我们的问题空间被假设为连续的，我们使用欧氏距离函数来计算空间中两点之间的距离。现在，我们制定一个约束，最小化总路径长度而不触碰障碍物。设$F$为一个确定轨迹长度的目标函数。

对于图2中具有位置$(x_r, y_r)$的粒子，它代表了机器人的下一个潜在位置解决方案

$$F=\sqrt{(x_r-x_i)^2+(y_r-y_i)^2}+\sqrt{(x_i-x_g)^2+(y_i-y_g)^2}\tag{5}$$

从图2可以得到：

$$x_i=x_r+V_rcos\theta_i\tag{6}$$ $$y_i=y_r+V_rsin\theta_i\tag{7}$$

因此

$$F=V_r+\sqrt{(x_r+V_rcos\theta_i-x_g)^2+(y_r+2V_rsin\theta_i-y_g)^2}\tag{8}$$

为了考虑环境中的静态和动态障碍物，我们将一个惩罚函数添加到目标函数(8)中。因此，当前的约束优化问题被转化为：

$$F=V_r+\sqrt{(x_r+V_rcos\theta_i-x_g)^2+(y_r+2V_rsin\theta_i-y_g)^2}+Penalty(i)\tag{9}$$

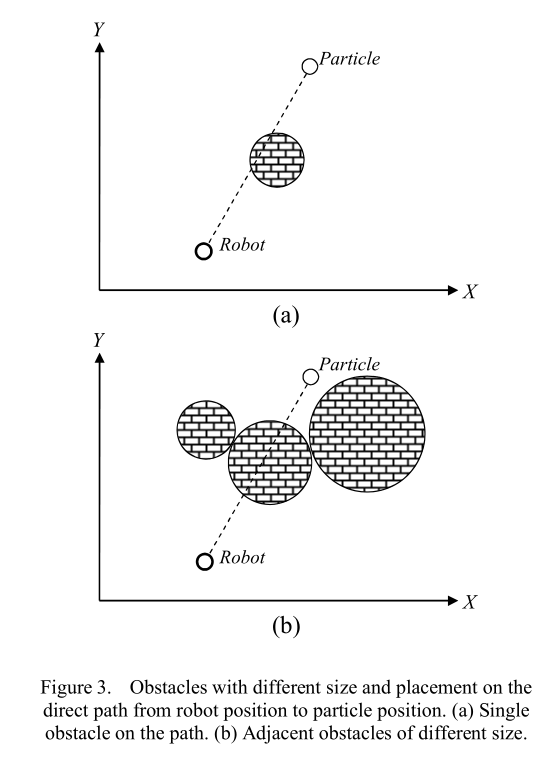
以前的研究使用了静态的惩罚函数，作为一个正常数，当路径上存在障碍物时就会应用，而不考虑障碍物的大小和它相对于所谓的路径的位置[4]。然而，在一个环境中，障碍物和目标的可移动性对选择适当的轨迹产生影响时，不仅路径上存在障碍物很重要，而且在评估轨迹时还需要考虑障碍物的大小和相对于路径的位置（见图3）。在下一节中，我们将提出一个基于环境状态的动态惩罚函数，克服静态版本的缺点。

4、提出的方法

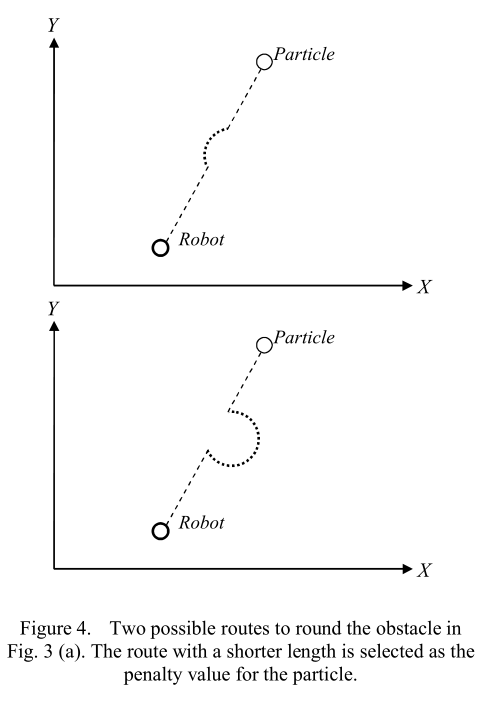
在本节中，我们首先提出了一种最适合动态环境的新型惩罚函数，以解决约束优化问题。所提出的惩罚函数观察了阻碍轨迹的障碍物的大小和位置，并试图根据这些参数找到通往目标的最短路径，从而确保不会陷入局部最优解。与[4]中讨论的方法不同，这种新方法不会陷入局部最优解，而且总是能够找到路径（如果存在的话）。为了计算粒子的惩罚值，首先我们找到了从机器人到粒子的直接路径与障碍物的两个交点。如图4所示，这将障碍物分为两部分。这意味着机器人可以在第一个交点处朝任一方向旋转以绕过障碍物并到达第二个交点。但机器人选择较短路径是合理的。因此，计算两部分的成本（弧长）并选择较小的那一个作为惩罚值。检查环境中的所有障碍物，看是否可能与机器人到粒子的直接路径发生碰撞，如果有任何碰撞，就计算相应的惩罚值并添加到总惩罚中。

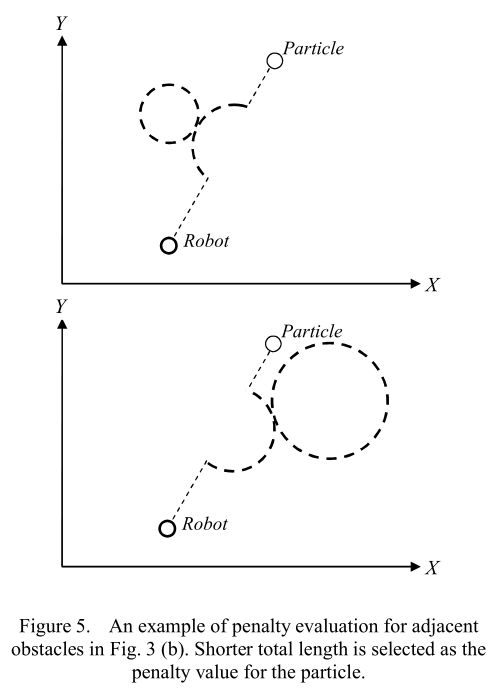
尽管根据第三节中的预设条件，两个障碍物不能重叠，但它们可以相邻，从而阻止机器人朝着目标穿越它们。对于这种类型的障碍物，在计算阻挡障碍物的两个部分的弧长时，相邻障碍物（们）的周长被添加到该部分的弧长中。这种情况的示例如图5所示。

最后，对于粒子与目标之间的路径，进行相同的过程，如果直接路径与任何障碍物发生碰撞，那么惩罚值将以相同的方式计算并添加到该粒子的总惩罚值中。

这个过程可以总结为公式(10)，作为第$i$个粒子的惩罚函数：

$$Penalty(i)=min\{\bar{arc}_j+\sum^S_{s=1}Circumference(s)|j\in \{1,2\}\}\tag{10}$$

其中，$S$是具有${arc}_j$的相邻障碍物的数量，$Circumference$是一个递归函数，用于计算相邻障碍物的周长。

5、使用PSO解决约束路径规划问题

在本节中，我们提出了一种使用PSO解决第三节中介绍的约束路径规划问题的方法。
所提出的方案假设了机器人的当前位置、障碍物和目标，以及问题相关的参数，并通过优化给定的约束目标函数来确定机器人的下一个位置。
轨迹规划算法的步骤可以总结如下（算法2）：

• 步骤1：将机器人的当前位置添加到轨迹中。
• 步骤2：如果机器人的当前位置与目标之间的距离小于或等于预定义的阈值，则转到步骤6。
• 步骤3：根据其对应的重新定位概率和速度移动障碍物和目标。
• 步骤4：在机器人的当前位置周围初始化PSO群体。根据算法1演化PSO群体。
• 步骤5：选择PSO群体的$gbest$位置作为机器人的当前位置，然后返回到步骤1。
• 步骤6：将目标位置添加到轨迹中并停止。