移动机器人路径规划的粒子群优化增强方法
移动机器人路径规划的粒子群优化增强方法
K. Sarkar, B. K. Balabantaray, A. Chakrabarty, B. B. Biswal and B. Mohanty, “Path Planning of Mobile Robots Using Enhanced Particle Swarm Optimization,” 2020 3rd International Conference on Energy, Power and Environment: Towards Clean Energy Technologies, Shillong, Meghalaya, India, 2021, pp. 1-6, doi: 10.1109/ICEPE50861.2021.9404505.
摘要
随着技术的迅猛发展以及机器人的广泛应用,自主移动机器人在工业和研究领域中受到了极大的关注。其中一个关键问题是找到一条无碰撞的路径,机器人可以通过这条路径到达目的地。本文提出了一种基于进化优化的自主路径规划方法用于移动机器人。我们引入了一种自适应适应度函数,它考虑了路径规划过程中的三个关键方面:(i)路径中的障碍物避让(ii)选择较短的路径长度和(iii)选择较平滑的路径。粒子群优化(PSO)算法被用来优化适应度函数。通过所提出的适应度函数优化目标函数,能够在各种障碍物存在的情况下,从起始位置生成一条平滑且无碰撞的路径到达目的地。进行了大量的模拟实验来验证我们所提工作的性能。将我们所提出的工作的性能行为与一些现有的最先进的基于优化的路径规划方法进行了比较,结果显示我们的方法能够产生更优越的结果。
I. 引言
在机器人技术领域中,移动机器人的路径规划已经成为一项重要任务。移动机器人的应用范围已经涉及诸多领域,如医学科学、空间研究、教育、农业、军事任务等,执行一些关键的无人任务,如排除炸弹、自动驾驶汽车等等。路径规划问题包括四个子问题,即(i)感知,(ii)定位,(iii)路径确定以及(iv)运动控制。在这些任务中,定位和路径确定是最关键的任务。
路径规划问题(PPP)被描述为确定一条短且无碰撞的路径,该路径将机器人从一个位置逐渐引到期望位置,同时要避开环境中的障碍物。一个合适的路径规划算法需要满足一些附加条件,如最小轨迹长度、轨迹安全,以及轨迹应该足够平滑。
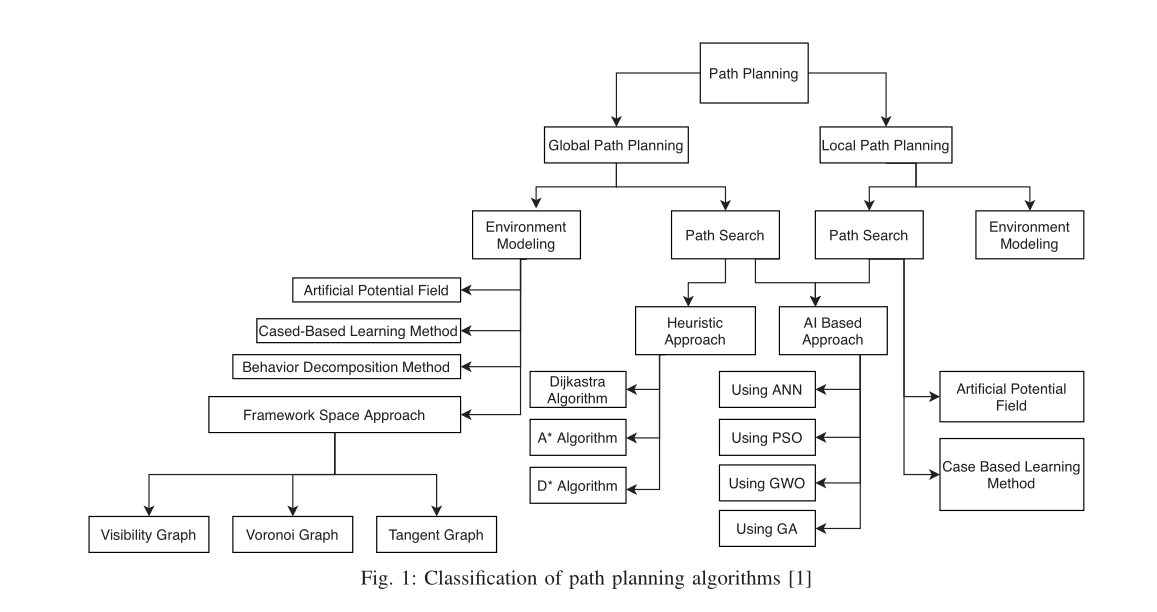
通常,路径规划问题分为两类:(i)全局路径规划和(ii)局部路径规划。在全局路径规划中,环境的完整信息是已知的,基于这些信息,在机器人开始移动之前就生成完整的路径[1]。机器人在整个路径生成后开始沿着路径移动。这也被称为离线路径规划。而在局部路径规划或在线路径规划中,机器人要么没有信息,要么可能对环境有不完整的信息。在自主机器人移动过程中,信息是通过部署在机器人身上的传感器收集的。在局部路径规划中,整个路径不是在机器人开始移动之前就生成的。每一时刻都在决定一小部分路径。全局路径规划方法从来不保证提供最优路径,因为环境中存在不确定性。相反,它可以承诺提供接近最优的路径。图1中给出了各种路径规划算法的层次分类。
在过去的几十年里,许多技术[2, 3, 4, 5, 6, 7, 8, 9]已经被开发出来,以解决移动机器人的路径规划问题。这些方法利用了各种进化优化算法来规划移动机器人的最优路径。在[2, 3, 4]的方法中,作者提出了使用遗传算法(GA)来解决路径规划问题。作为进步,在[3]中的方法作者利用基于GA的算法,使用可变长度的基因/染色体表示来建模PPP。优化过程旨在最小化从初始位置到目标位置的能耗。在每个染色体中,第一个节点包含机器人的起始位置,最后一个节点包含机器人的目标位置。中间节点除开始和目标节点外,都对路径有所贡献。此外,还考虑了两个安全级别,即第一安全级别(FSL)和第二安全级别(SSL)。
在[4]的方法中,作者使用了带有新的交叉概率和更好的初始种群的GA,以实现移动机器人的平滑路径。解决路径规划问题的另一个流行选择是使用蚁群优化(ACO)技术。在这项工作[5]中,作者使用网格图表示来代表环境。在基于网格图的表示中,整个环境被划分为小网格,并且这些网格被分类为自由网格和障碍物网格。机器人的路径是一系列网格。在遵循特定网格序列后,如果蚂蚁与任何障碍物网格相撞,则该网格序列被标记为不可行的路径。在[6, 7, 8]的方法中,作者利用了PSO进行PPP,并且表现出比基于GA的PPP更好。在[8]中提出了PSO与另一个定制的坐标生成算法结合使用,并且发现这种方法能够在任何已知环境中避免局部最小值。在[9]的方法中,作者利用了随机PSO,使其能够为移动机器人生成非平滑路径。然而,除了进化优化算法之外,还提出了基于神经网络的路径规划概念[10, 11, 12, 13]。
在本文中,我们提出了一种自动化的路径规划方法,通过最小化移动机器人在存在三个或四个障碍物的环境中的偏离角来实现。与现有的传统基于PSO的PPP不同,我们在这里利用了一个增强的适应度函数,由PSO来优化。所提出的适应度函数考虑了三个关键方面:(i)路径中的障碍物避让(ii)选择较短的路径长度和(iii)路径规划过程中较平滑路径的选择。通过建议的适应度函数优化目标函数,能够在各种障碍物存在的情况下,从初始位置生成一条更平滑且无碰撞的路径到目的位置。
本文的其余部分组织如下:第2节简要描述了PSO算法的基础。通过修改的PSO描述的路径规划在第3节中。第4节提供了与现有的最先进的基于进化优化算法的路径规划方法相比的所提出工作的结果和分析。最后,第5节讨论了总结和一些未来的方向以提高建议工作的性能。
II. 粒子群优化(PSO)
粒子群优化(PSO)是一种用于优化非线性连续函数的方法[14]。PSO的灵感来源于诸如成群结队的鱼或鸟群飞行时的社会行为。PSO直接实施起来简单,并且可以有效地找到最优或近乎最优的解[6, 7]。PSO的三个主要步骤是:
1) 为每个粒子计算适应度值。
2) 更新每个粒子的局部最佳位置以及群体中迄今为止找到的全局最佳位置。
3) 更新每个粒子的位置和速度。
PSO的主要机制是在粒子群体之间共享知识。每个粒子都在搜索空间内寻找最佳解。这一搜索过程由每个粒子的个体知识以及整个粒子群的知识所引导。PSO是一种迭代算法。在每次迭代中,每个粒子都试图朝最佳解靠近。每次迭代后,都会记录群体迄今为止发现的最佳解。每个粒子的速度和位置通过公式(1)和公式(2)更新。一个粒子在两次迭代之间的位置移动被称为速度。
在这里,$i$是粒子的索引,$k$是迭代次数。因此,$V^k_i$是第 $k$次迭代时第 $i$个粒子的速度,$P^k_i$是第 $k$次迭代后第 $i$个粒子的最佳位置,$X^k_i$是第$k$次迭代时粒子$i$的位置。$P^k_g$是第$k$次迭代后的全局最佳位置。$\omega$是惯性权重。$c_1$和 $c_2$是加速系数。$r_1$和 $r_2$是在 $[0,1]$ 范围内的随机值。
III. 使用PSO进行路径规划
在机器人的起始位置和目的地之间存在障碍物,这增加了路径规划问题的复杂性。如果起点和终点之间没有障碍物,机器人可以直接沿直线从起点到终点以到达目标。我们的路径规划算法旨在当存在障碍物时选择一个替代路径。在这种方法中,机器人最初开始朝目标直线移动,从初始位置到目标位置。一旦机器人感知到此路径中存在障碍物,便启动PSO来确定将通过其替代路径的最佳替代点。该点是基于最小适应度值标准计算得出的,这个点被称为全局最佳位置。确定全局最佳位置后,机器人朝该全局最佳位置偏转,以避免与障碍物碰撞。这个过程持续迭代,直到满足终止条件。
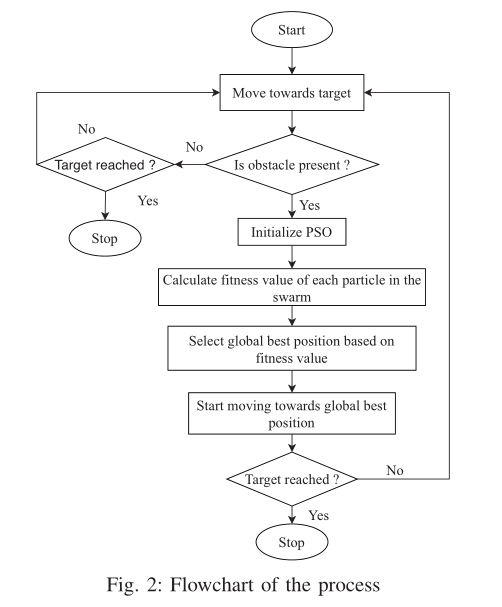
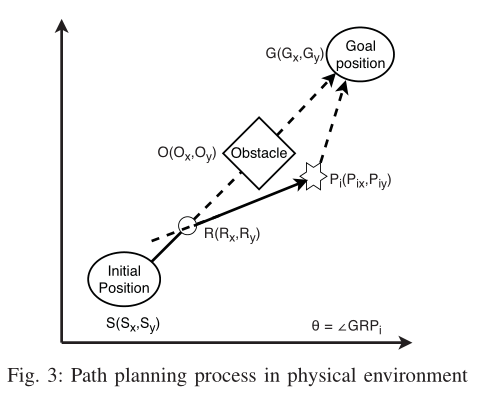
终止条件是PSO达到了最大迭代次数,或者机器人已经到达目的地,或者没有可能的路径。整个过程的流程图在图2中给出,它详细阐述了整个过程。现在,让我们讨论在实际环境中移动机器人的路径规划。图3描绘了在环境中存在障碍物的情况下,移动机器人从任意起始位置到目标/目的地位置的路径规划的示意图。设$S(S_x,S_y)$和$G(G_x,G_y)$是移动机器人的起始位置和目标/目的地位置。设机器人从位置$S(S_x,S_y)$开始移动到当前位置$R(R_x,R_y)$。假设在当前位置,机器人在环境中没有感知到障碍物。因此,它将遵循最短长度路径,即从初始位置到最终位置的直线路径。相反,如果当前位置机器人感知到最近的障碍物$O(O_x,O_y)$的存在。一旦感知到障碍物,移动机器人必须从直线路径偏离,沿$RP_i$路径以角度$θ=∠GRP_i$转向位置$P_i(P_{ix},P_{iy})$,这个角度称为偏转角。偏转角是机器人在当前路径中存在障碍物时转向的角度。$p_i$是通过PSO算法获得的全局最佳第$P_i$粒子。偏转角$θ=∠GRP_i$越小,移动机器人的路径就越平滑。因此,我们的路径规划方法旨在通过使用PSO来最小化偏转角$θ$,以实现更平滑且无碰撞的路径。方程(3)提供了我们提出工作的目标函数。
为了使用粒子群优化(PSO)解决路径规划问题,首先通过定义适当的适应度函数将路径规划问题转换为优化问题。设定好适应度函数后,使用PSO来检测全局最优粒子$p_i$。全局最优粒子是基于最优(最小)适应度值来选择的。下面的小节讨论了我们优化过程中要包含的适应度函数。
A. 适应度函数的构建:
在我们的提议工作中,我们设计了适应度函数作为三个独立适应度函数的加权线性组合,用 $F_{final}(.)$ 表示。方程(4)描述了优化过程中 $F_{final}(.)$ 的构建。
其中,$F_1(.)$、$F_2(.)$ 和 $F_3(.)$ 是独立的适应度函数。$\omega_1$、$\omega_2$ 和 $\omega_3$ 是与各个适应度函数相关联的权重。
优化方程(3)中描述的目标函数,通过利用建议的适应度函数 $F_{final}(.)$可以实现三个主要方面:(i)路径中的障碍物避让(ii)更短的路径长度以及(iii)路径的平滑追踪。
1) 适应度函数 $F_1(.)$:适应度函数 $F_1(.)$用于确保碰撞障碍物。为了避免碰撞障碍物,通过确保与最近障碍物的最大距离来选择全局最优粒子。因此,适应度函数 $F_1(.)$与全局最优粒子$P_i(P_{ix},P_{iy})$的位置与最近障碍物位置$O(O_x,O_y)$之间的距离成反比。方程(5)描述了适应度函数 $F_1(.)$的构建。
当选择最小适应度值的粒子作为全局最优粒子时,会在障碍物和机器人之间产生排斥力。这种排斥力保护了机器人不会与障碍物碰撞。
2) 适应度函数 $F_2(.)$:当路径长度更短时,机器人将更快地到达目标。适应度函数$F_2(.)$确保路径长度短。函数$F_2(.)$与全局最优粒子$P_i(P_{ix},P_{iy})$与目标位置$G(G_x,G_y)$之间的距离成正比。全局最优粒子与目标位置之间的距离产生了目的地和机器人之间的吸引力。这种吸引力引导机器人朝向目的地,如方程(8)所描述。
3) 适应度函数 $F_3(.)$:适应度函数$F_3(.)$能够为移动机器人提供更平滑的路径。当偏差角度较小时,机器人的路径会更加平滑。在这种情况下,机器人被偏离了$θ=∠GRP _i$,因此适应度函数$F_3(.)$应该与偏离角$\theta$成正比,如方程(11)所描述。
在图3中,$\theta$是线段$RG$和$RP_i$之间的锐角。因此,$\theta$可以由这两条线段的斜率表示。设线段$RG$的斜率为$m_1$,线段$RP_i$的斜率为$m_2$。斜率$m_1$是线段$RG$在$X$轴变化时$Y$轴的变化。因此,$m_1=\frac{G_y-R_y}{G_x-R_x}$,相似的,$m_2=\frac{P_{iy}-R_y}{P_{ix}-R_x}$,那么$\theta$可以由公式(13)计算